NIK SZTF Záróvizsga tételek
A 2020-21. félévtől érvényben lévő tétellista alapján.
Források, jegyzetek, anyagok
- Dr. Kertész Gábor: Párhuzamos és elosztott rendszerek programozása
- Dr. Szénási Sándor: Haladó Algoritmusok
- CUDA Trainings
- SZFI E-learning videók
- Sima Dezső, Szénási Sándor: GPGPU-k és programozásuk
- PERProg anyagok
Utoljára frissítve: 2024.01.20.
1. tétel - Párhuzamos programok hatékonysága
Ismertesse Amdahl és Gustafson törvényét! Definiálja az overhead és a bottleneck fogalmakat! Mutassa be a szemcsézettség és terheléselosztás kapcsolatát!
Egy szekvenciális program futásideje formálisan felírható mint:
\[ T_{total} = T_{setup} + T_{compute} + T_{finalization} \]
Ahol:
- setup: inicializációs lépések
- pl: adatbetöltés, memória foglalás, hálózati kapcsolat
- nem párhuzamosítható
- compute: konkrét feladat végrehajtása
- finalization: lezárás
- pl: eredmények mentése, hálózaton való továbbítása
- nem párhuzamosítható
A futásidő p darab műveletvégző esetén
\[ T_{total}(p) = T_{setup} + \frac{T_{compute}}{p} + T_{finalization} \]
Amdahl törvénye
- Gene Amdahl 1967-ben publikálta
- Azt modellezi, hogy egy szekvenciális program párhuzamos implementációjának futtatása esetén milyen kapcsolat jelenik meg a processzorok száma és a várható sebességnövekedés között.
A publikált képlete:
\[ S_{latency}(p) = \frac{1}{{(1-f)+\frac{f}{p}}} \]
- Slatency(p): elméleti gyorsulás. A latency itt látenst jelent, nem késleltetést!
- p: műveletvégzők száma
- f: program párhuzamosítható szakasza (0 és 1 közötti szám)
Fontos következtetések:
- p és Slatency(p) közötti összefüggés nem lineáris
- tehát pl. 2x annyi műveletvégzőtől nem lesz 2x gyorsabb
- a gyorsítás mértéke mindig kisebb, mint a műveletvégzők száma
- fix feladatméretet feltételez, azaz, az erőforrások növelésével nem változik a terhelés, nem lesz nagyobb a feladat, ugyanazt kell megoldani
Bottleneck
- Minden olyan kódblokk, amely szekvenciálisan kell, hogy végrehajtódjon, az rontani fogja az összteljesítményt.
- Bottleneck-ek: a szoftverfejlesztésben azon a komponensek, amelyeknek az áteresztőképessége alacsony, és ez korlátozza a teljes rendszer teljesítményét
Overhead
Az időmennyiség párhuzamos programozásnál, amely a probléma megoldása szempontjából "haszontalan" feladatokkal telt, melyek szekvenciális esetben nem fordultak volna elő.
Például:
- Műveletvégzők kezelése
- Műveletvégzők közötti kommunikáció időben adott költsége
Amdahl törvénye nem veszi figyelembe a párhuzamosításhoz implementálandó
esetleges további utasításokat, és az ezek végrehajtásához szükséges időt. Ha ezt is figyelembe vennénk, akkor a teljes időhöz megjelenne egy Toverhead tényező, amely p értékével arányos.
Az overhead mértéke függ:
- a konkrét algoritmustól
- környezettől
- konkrét implementációtól,
de \(T_{overhead}(p) = log_{2}(p) \) egy jó közelítés.
Gustafson törvénye
Megadja, hogy ha egy p darab műveletvégzővel rendelkező párhuzamos gép t idő alatt oldaná meg a problémát, akkor mennyi ideig tartana egyetlen szekvenciálisnak.
Gustafson szerint az elméleti elérhető gyorsítás megadható, mint
\[ S_{latency}(p) = 1 - f + pf \]
A szemcsézettség és terheléselosztás kapcsolata
A dekompozíció célja a feladat kisebb, konkurens módon végrehajtható részfeladatokra bontása.
A szemcsézettséggel a részfeladatok méretét és mennyiségét írjuk le.
| Finoman szencsézett | Durván szemcsézett | |
|---|---|---|
| Feladatok száma | sok | kevés |
| Feladatok mérete | kicsi | nagy |
| Hátrány | Overhead mértéke jelentős, ami negatív hatással lehet a teljesítményre | Részfeladatok méretbeli eltérése lehet jelentős => negatív hatás a műveletvégzők kihasználtságára |
- A feladat végrehajtása közben az az elsődleges cél, hogy az elérhető műveletvégzők végig kihasználtan dolgozzanak.
- Ideális esetben az összes műveletvégző egyszerre végez, ezzel előállítva a végeredményt, ellenkező esetben az utolsó még dolgozó műveletvégzőt kell bevárniuk a már végzett szálaknak.
Terheléselosztás: a műveletvégzők közötti hatékony kihasználtság elérése
Cél: minden műveletvégző egyszerre végezzen a feladatával.
A szemcsézettség és a terheléselosztás kapcsolódik egymáshoz, ugyanis finoman szemcsézett részfeladatok között kisebbek a különbségek, durva szemcsézettség esetén nagyobbak, ez utóbbi pedig kevésbé hatékony terheléselosztást eredményezhet. Finom szemcsézettség esetén pedig az overhead mértéke lesz jelentős, ugyanakkor hatékonyabb terheléselosztás valósítható meg.
2. tétel - Szinkronizáció I.
Ismertesse Dekker és Peterson algoritmusát kölcsönös kizárásra! Mire szolgál és milyen elven működik Lamport Bakery algoritmusa?
A kód azon részét, ahol a közös, függést okozó változók vannak, kritikus szakasznak nevezzük. Cél: a kritikus szakaszban egyszerre csak egy szál legyen.
Dekker algoritmusa
- Két szál verseng, hogy a kritikus szakaszba léphessen
- Az algoritmus a szál indexétől függően eltérően viselkedik.
flag[i]true értéket vesz fel, ha aziindexű szál be kíván lépni a kritikus szakaszba- Ha a szálak egyszerre kezdik meg a belépést, akkor a
turnváltozó értéke jelzi, hogy melyik szál következik


- A
0indexű szál aflag[0]értékét igazra állítja, és megvizsgálja aflag[1]értékét. - Ha hamis, akkor a szál belép a kritikus szakaszba. Kilépéskor pedig visszaállítja hamisra a saját flagjét.
- A gyakorlatban a
turndönt a belépésről azokban az esetekben, amikor a belépést a szálak esetleg egyszerre kezdik meg: aturnértéke jelzi, hogy mely szál következik; a másik szál várakozik. - Ha a
turnazt jelzi, hogy a másik szál van soron, akkor a szál leveszi a flagjét, és várakozik aturnmegváltozására. Fontos észrevenni, hogy a flag hamisra állítása fontos lépés, hisz a másik szál esetlegesen ezt vizsgálja a belépési protokolljában, így nem léphet be amíg aztrueértékű.
Előfordulhat olyan eset, hogy:
T₀a kritikus szakaszban van, T1 várakozikT₀a kilépés után egyből belépést kezdeményez, T1 nem tud időben kijönni a várakozó állapotból. Ekkor sérül a fair kiszolgálás.
Peterson algoritmusa
- A
turnváltozó a belépési feltétel részeként szerepel - A
flagátállítását követően aturna másik szálra fog mutatni, hogy az következik a sorban. - Ebben az eseten megfigyelhető a fair
viselkedés, vagyis amelyik szál hamarabb kezdi meg a belépést, garantáltan az fog előbb belépni a kritikus
szakaszba. Ekkor ugyanis a
turnérvényes értéke az utolsó beállított érték lesz.

Lamport algoritmusa
Lamport Bakery algoritmusa több szál kölcsönös kizárását hivatott megoldani, amely a pékségekben használt várósoron alapul.
- Minden szál egy sorszámot kap, és mindig a legkisebb sorszámú kerül kiszolgálásra, addig a többi várakozik.
- Az algoritmusban előre ismert a szálak száma.
- Kezdetben minden szám egy sorszámot kap, eggyel nagyobbat az utolsónál.
- Van egy
choosingtömb.choosing[i]igaz, ha aziindexű szál még nem kapott sorszámot. - Amíg a choosing tömb bármelyik eleme igaz, a szálak várakoznak,tehát megvárják, hogy minden szál sorszámhoz jusson.
- A várakozás megvalósításában, ha egy
Bszál már a belépési protokollban vagy a kritikus szakaszban tartózkodik, és a sorszáma kisebb, vagy egyező és az indexe kisebb, mintAszálnak, akkorAszál várakozni kényszerül.
3. tétel - Szinkronizáció II.
Mutassa be a szemafor és a monitor működését! Milyen esetekben célszerű a használatuk?
Szemafor
A szemafor két atomi műveletből (P() és V()), valamint egy várósorból és egy S változóból álló szinkronizációs szerkezet. A kritikus szakasz P() és V() művelet között helyezkedik el. S kezdőértéke kölcsönös
kizárás esetén 1, mely értékét a belépni szándékozó szálak csökkenthetik.

Az első P() csökkenteni próbálja S értékét, ezzel a többi szál
várakoztatásáért felel. Ha az S változó értéke negatív lett, akkor van már szál a kritikus szakaszban, esetleg már több szál is várakozik, tehát a szál bekerül a Q várósorba. Egyébként, ha S értéke nem kisebb mint 0, akkor
a szemaforban még van férőhely, tehát a szál beléphet a kritikus szakaszba.
A V() növeli S értékét. Ha az 0, vagy annál kisebb, van várakozó szál a sorban. Ekkor értesíti a legrégebbóta váró szálat, hogy beléphet a kritikus szakaszba.


Bináris szemafor esetén S kezdőértéke 1, ekkor, ha S értéke 0, akkor biztosan az adott szál csökkentette a S
értékét, tehát üres a kritikus szakasz.
Ha a várósor FIFO, akkor erős szemafor, fair kiszolgálással.
Szemafor használata akkor célszerű, ha a kritikus szakaszban egyszerre több szál is tartózkodhat, de ezeknek a száma felülről korlátos kell legyen.
Monitor
A monitor egy szinkronizációs szerkezet, ami egy lockon (L) és egy feltételváltozón (CV) alapul. Ezzel az eszközzel a szálak
blokkolását egy feltételhez tudjuk kötni, tehát olyan kölcsönös kizárást valósít meg, ahol feltételhez kötött a belépés a kritikus szakaszba.
A CV feltételváltozó (Condition Variable) egy olyan sor struktúrájú szerkezet, amelyre a szálak feliratkozhatnak, ha a feltétel kiértékelése nem megfelelő számukra a továbblépésre. A feliratkozott szál értesítésig blokkolódik.
Három atomi művelete van, ezek a wait, a signal és a broadcast.
A wait művelet a feltételváltozó blokkoló viselkedését valósítja meg. kiértékeli a feltételváltozót (CV), és ha szükséges, akkor a szál feliratkozik a CV értesítéseire, blokkolódik és
elengedi a lockot. (A feltétel kiértékelése,
és a feltételváltozóra való feliratkozás maga egy lockkal őrzött kritikus szakaszban történik).
A signal és a broadcast a blokkolt szálak értesítésére szolgálnak a feltételváltozón keresztül, előbbi csak egyet (a legrégebb óta váraakozót), az utóbbi az összeset felébreszti a blokkolásból.

4. tétel - Holtpont
Mutassa be az étkező filozófusok problémáját! Definiálja a holtpont fogalmát! Mik a kialakulásának előfeltételei? Ismertesse a kezelésének módszereit!
Étkező filozófusok
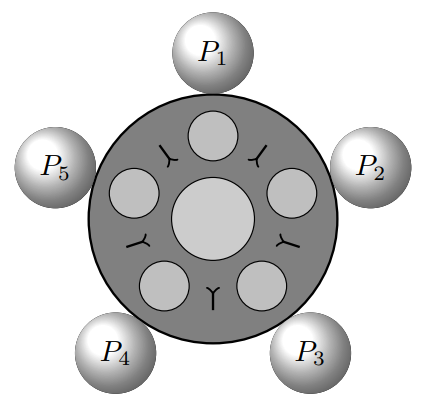
-
Öt filozófus ül egy kör alakú asztalánál
-
Ténykedésük során a filozofálás és étkezés műveleteket végzik végtelen sokáig, felváltva.
-
Az étkezéshez két villa kell egy filozófusnak, mert spagettit esznek
-
A gondolkodáshoz nem kell semmi
-
Az asztalnál pontosan annyi villa van, mint amennyi filozófus, ezek két-két filozófus közé vannak elhelyezve
Megkötések:
- Az erőforrások nem megoszthatóak: egy villát egy filozófus használ egyszerre
- Egy filozófus csak addig tartja magánál a villát, amíg eszik
- Ha a filozófus megéhezik, de a bal vagy jobb-oldali villa foglalt, akkor várakozik annak felszabadulására
- A filozófusok önállóak, nem kommunikálnak
Előfordulhat, hogy minden filozófus rögtön éhes, és felveszi a tőle jobbra lévő villát. Ekkor nincs ütközés, mindenki fel tud venni egy villát. Mivel két villa kell az evéshez, mindegyikük nyúlna a bal villáért is. Mivel azonban az már a tőlük balra ülő filozófus kezében van, várakozni kezdenek a felszabadulásra, ami soha nem következik be, mert mindenki a tőle balra ülőre vár. Ez a helyzet a holtpont.
Holtpont
Általánosságban holtpontról akkor beszélünk, ha egy szál blokkolva van, és annak blokkolása sosem szűnik meg.
Szálak vagy folyamatok halmaza holtpontban van, ha mindegyik vár egy olyan esemény bekövetkeztére, amelyet ugyanezen halmaz egy másik eleme válthat ki. Az elemek egymásra várakoznak, tehát a várakozás sosem fog véget érni
Holtpont kialakulásának feltételei
- Körkörös várakozás
- Kölcsönös kizárás: közös, nem megosztható erőforrások
- Foglal és vár stratégia: egy szál munkájához több erőforrásra is szükség van, és magánál tartja őket az összes megszerzéséig
- Preemptivitiás hiánya: egy felsőbb szintű felügyelő nem tudja elvenni az erőforrást a száltól
Holtpont kezelése megelőzéssel
A 4 közül az egyik szükséges feltételt megszüntetjük, így nem állhat elő holtpont
- A kölcsönös kizárás elkerülése nem biztonságos, mert megosztottak az erőforrások
- A foglal és vár megszüntetéséhez a szálnak el kellene engednie a már megszerzett erőforrást, hogy egy újat szerezzen meg. Ezesetében ismerünk kell előre az erőforrásokat, és fennáll a kiéheztetés veszélye.
- A preemtivitás esetén beláthatatlan következményei lehetnek, ha egy szál elveszíti az erőforrást
- Legkönnyebben tehát a körkörös várakozás szüntethető meg
- Korlátozzuk, hogy egy szál egyidőben legfeljebb csak egy erőforrást tarthat magánál
- Nem mindig lehetséges, mert van hogy több erőforrás kell
- Erőforrás kérés szabályozása, pl. az erőforrások sorbarendezésével
- Az étkező filozófusoknál például 1-től 5-ig számozzuk a villákat, és megkötjük, hogy előbb a kisebb számú villát kell felvenni a filozófusnak. Ekkor:
- filozófus célja: R1 majd R2 megszerzése
- filozófus célja: R2 majd R3 megszerzése
- filozófus célja: R3 majd R4 megszerzése
- filozófus célja: R4 majd R5 megszerzése
- filozófus célja: R1 majd R5 megszerzése
- Mivel az első és utolsó filozófus közül egyik nem tudja megszerezni R1-et, nem alakul ki holtpont
- Az étkező filozófusoknál például 1-től 5-ig számozzuk a villákat, és megkötjük, hogy előbb a kisebb számú villát kell felvenni a filozófusnak. Ekkor:
- Korlátozzuk, hogy egy szál egyidőben legfeljebb csak egy erőforrást tarthat magánál
Holtpont kezelése elkerüléssel
Futásidőben figyeljük, hogy olyan erőforrás hozzárendelés ne történhessen, amely holtponthoz vezethet. Erőforrás igénylésekor a felügyelő szerv elvégez egy számítást, mi történne, ha a kérést engedélyezné, biztonságos (holtpont nélküli) vagy nem biztonságos (holtpont) állapotba kerülne-e.
Ha biztonságos lenne, engedélyezi az erőforrás-kérést, ha nem, akkor blokkolja a kérést addig, amíg nem lesz biztonságosan teljesíthető.
Holtpont kezelése észlelés és helyreállás által
Erőforrás-foglalási gráf
Olyan irányított gráf, ahol a csomópontok szálakat (P) és erőforrásokat (R) jelölhetnek. A gráf élei minden esetben csak szálak és erőforrások között vezethetnek.
- Ha egy szál csomópontjából él vezet egy erőforrás csomópontjába, akkor a szál igényli az erőforrást.
- Ha egy erőforrás csomópontjából él vezet egy szál csomópontjába, akkor a szál magánál tartja az erőforrást.
Észlelés
- A holtpont felfedezése a gyakorlatban megoldható az erőforrás-foglalási gráf megtekintésével.
- Ha a rendszerben nincs több példányt kiosztó erőforrás, és a szükséges feltételek mellett irányított kört figyelünk meg, akkor a rendszer holtpontba került.
- Amennyiben az érintett erőforrások több példány kiadására is képesek, akkor a kör nem igazolja a holtpont meglétét. Ilyen esetben egyéb feltételek megvizsgálása is szükséges lehet.
Helyreállás
- valamely szálat vagy szálakat meg kell szakítani, és az általuk foglalt erőforrást felszabadítani
- gyors, de költséges megoldás, ha minden érintett szálat megszakítunk
- megszakíthatunk csak egy-egy szálat is, de melyiket?
- erőforrás-foglalási gráf elemzése segíthet
- vagy egyesével szakítjuk meg a szálakat addig, amíg a holtpont meg nem szűnik (akár valamilyen prioritás alapján sorrendben => mohó módszer)
5. tétel - Konkurens adatszerkezetek I.
Mutassa be a termelő-fogyasztó problémát! Definiálja a szálbiztos adatszerkezet fogalmát! Sor adatszerkezet esetén milyen módszerrel érhető el a szálbiztosság?
A tételhez érdemes elolvasni az Alíz-Bob kutyás sztorit is (itt), szerintem segíti a megértést.
Termelő-fogyasztó probléma
Helyzet
- Egy adatszerkezet áll a középpontban
- a termelő behelyez elemeket
- a fogyasztók pedig eltávolítanak elemeket
- A termelő csak akkor végezheti a tevékenységét, ha a fogyasztók éppen nem fogyasztanak
- Cél:
- Nem akarjuk, hogy a termelő a fogyasztókra várakozzon
- A fogyasztókat maximálisan ki akarjuk használni
- Megoldás: egy buffert használunk, amely egy sor adatszerkezetként is értelmezhető
- A termelő behelyezi a sorba az elemeket, a fogyasztók pedig kiveszik
- A buffer mérete véges, tehát ha tele a sor, akkor a termelő várakozik, ha pedig üres, akkor a fogyasztók.
- A termelő jelez a fogyasztóknak, ha behelyezte az első elemet
- A fogyasztók jeleznek a termelőnek, ha kivették az utolsót
Probléma
- Megtelik a buffer, a termelő leáll, de a fogyasztók már ki is ürítik a sort, és hamarabb jeleznek a termelőnek, mint az elkezdett volna várakozni.
- Ekkor felek egymásra várnak, holtpont alakul ki.
- Ha a buffer elérése nem atomi művelet, akkor az is okozhat problémát
- Megoldható: szemaforral
- Ekkor a termelő egy szemaforba próbál belépni, ha a buffer nincsen tele.
- Siker esetén belehelyez egy elemet a tárolóba, és kilép a szemaforból.
- A fogyasztó belép egy szemaforba, ha a bufferben van elem, ekkor azt eltávolítja, és kilép a szemaforból.
- Több fogyasztó esetén a buffer elérését lockba kell zárni.

Szálbiztos adatszerkezet
Szálbiztosnak akkor nevezünk egy adatszerkezetet, ha több szál szimultán kérésére is versenyhelyzettől mentes marad.
Szálbiztosság elérése sor adatszerkezet esetén
Korlátos sor
- A termelő-fogyasztó problémánál bemutatott FIFO buffer szinkronizációját kell megoldani
- szemaforral
- monitorral
- az elemszámot érdemes külön egész számként követni és mindig frissíteni
- kölcsönös kizárással
- atomi inkrementálás/dekrementálás műveletekkel
- első és utolsó elem referenciáját tárolni kell
- Durván szemcsézett megoldás: egy globális lock van
- Finoman szemcsézett megoldás:
ENQ()ésDEQ()műveletek konkurens elérhetőek, lehetőség van a sorhoz szimultán hozzáadni és onnan elemet levenni- ekkor két lock van,
EnqLockésDeqLock EnqLockmegszerzésével lehet beszúrni:- szabad helyek ellenőrzése
- ha van hely: beszúrás, majd
EnqLockelengedése- a beszúrás után ébreszteni kell a levétellel foglalkozó várakozó ágakat, ha a lista üres volt, amihez
DeqLockmegszerzése szükséges
- a beszúrás után ébreszteni kell a levétellel foglalkozó várakozó ágakat, ha a lista üres volt, amihez
- ha nincs hely:
EnqLockelengedése és várakozás
DeqLockmegszerzésével lehet kivenni:- várakozás, ha a sor üres
- kivétel
- szabad helyek számának frissítése
- ha teli volt, a blokkolt hozzáadó szálak ébresztése (
EnqLockmegszerzésével és jelzéssel)
Korlátlan sor
- eltekintünk a kapacitástól
- A finoman szemcsézett és a triviális durván szemcsézett megoldás mellett lehetőség van lock-mentes implementációra is
CompareAndSetatomi műveletekre alapozva a megoldást.- Ebben az esetben ügyelni kell arra, hogy a művelet közben változhat a sor releváns eleme (első vagy utolsó, művelettől függően)
- ekkor a
CompareAndSetkiértékelés fázisában hamis visszajelzést ad: ekkor ismét próbálkozni kell.
- ekkor a
- Ez egyfajta lusta-elvű megközelítés a blokkolás helyett.
- Ebben az esetben ügyelni kell arra, hogy a művelet közben változhat a sor releváns eleme (első vagy utolsó, művelettől függően)
6. tétel - Konkurens adatszerkezetek II.
Milyen módszerekkel készíthető szálbiztos lista? Mutassa be a durván és a finoman szemcsézett, valamint optimista és lusta szinkronizáció elvi megoldását!
Szálbiztos lista
Definiáljuk a láncolt listát olyan generikus adatszerkezetként, amelynél adottak
az Add(), Remove() és Contains() műveletek. Az egyes listaelemek esetén legyen elérhető az elem T típusú értéke, az elem kulcsa, és a következő listaelem referenciája.
Durván szemcsézett megoldás
- Minden hozzáférést ugyanaz a lock őriz
- Nem hatékony
- Ha a lock várósora FIFO, akkor kiéheztetésmentes
- Ha alacsony a versengés a hozzáférésért, akkor jó lehet, mert kicsi az overhead és könnyű az implementáció
Finoman szemcsézett megoldás
- A szerkezetet külön részegységekre bontjuk
- A listaelemek külön-külön kerülnek lockolásra, amikor műveletet végzünk rajtuk
- Ha a műveletnél csak a forráselemet lockoljuk, könnyen hibára vezethet a versenyhelyzet miatt
- Pl:
fej → a → b → clistában törölni akarjuka-t ésb-t párhuzamosan. Ehhez egyik szálnak afejmutatójáta-rólb-re kell állítani, míg a másik szálnakamutatójátb-rőlc-re. Ekkor a versenyhelyzet miatt előállhat olyan eset, hogybhelytelenül a lista része marad, ha csak a mutatót tartalmazó csúcsok vannak zárolva.
- Pl:
- Megoldás: hand-over-hand locking:
- referencia módosításakor vagy megszüntetésekor nem csak a mutató csúcsot lockoljuk, hanem a mutatott csúcsot is
- A lockolás és feloldás csúszóablakos módszerrel, átfedéssel kell történjen
- A sorrend mindenképp azonos kell legyen, minden művelet esetén, különben holtpont alakulhat ki
- Hátrány: sokáig blokkolhat olyan szálakat, amelyek csak bejárni akarják a listát
Optimista szinkronizáció
- előbb zárolás nélkül, blokkolásmentesen bejárjuk a listát
- megnézzük, van-e értelme továbblépni:
- törlés esetén: megvan az elem
- beszúrás esetén: nincs még ilyen elem
- ha van, akkor a két érintett csúcsot lockoljuk
- majd ellenőrizzük, hogy még mindig érintetlenek-e
- ha a validáció
- sikeres: a művelet elvégezhető
- sikertelen: újra be kell járni a listát, és újra próbálkozni
- ha a gyűjtemény nem módosul a bejárást követően, akkor hatékony és szálbiztos a szinkronizáció
- a validáció lépése hosszadalmas
Lusta szinkronizáció
- az optimista szinkronizáció validációs lépése lerövidíthető
- bevezetünk a listaelemek esetén egy
MARKEDnevű logikai mezőt- ez igaz értéket kap, ha az elemet kijelöljük törlésre
- a bejárás szemszögéből ami nem
MARKED, az elérhető a fejből kiindulva, amiMARKED, az valójában már nincs a gyűjteményben
ADD():- a beszúrandó elem helyét megtalálva a két szomszédos csúcsot lockolja, majd validál
- validáció esetén a elég a két elem
MARKEDmezőjének értékét és a referenciát megvizsgálni- logikai értékek hamisak => az elemek nincsenek törölve
- mutató az előbbi csúcsból utóbbiba mutat => szomszédosak
- vizsgálat után mehet a beszúrás a két elem közé
REMOVE():- először a törlendő elemet keressük meg blokkolásmentesen
- ha megvan, a törlendő elem és a megelőző elem referenciáját zároljuk
- az elem
MARKEDmezejét igazra állítjuk - az elemet kiláncoljuk
CONTAINS():- megkeresi az elemet
- ellenőrzi, hogy a
MARKEDmező hamis értékű
7. tétel: Párhuzamos tervezési minták I.
Mutassa be a Single Program - Multiple Data tervezési mintát! Ismertesse a tulajdonságait, az általános felépítését, valamint tipikus használati eseteit! Mutassa be a Loop Parallelism tervezési mintát!
Single Program - Multiple Data
Általános felépítése
-
Inicializálás
Lokális allokációs műveletek, ha szükséges akkor más szálakhoz való kapcsolódási pontok definiálása. Implementációtól függően eltérő rutinokat is jelent, de a memóriafoglalás és a kommunikációs csatornák létrehozása mindig megtörténik.
-
Egyedi azonosító
Minden szál egyedi azonosítóval rendelkezik, jellemzően 0-tól indexelve. Az azonosításon túl meghatározhatja a szál viselkedését.
-
Végrehajtás
A szálak adatoktól és azonosítójuktól függően végrehajtják ugyanazokat az utasításokat. Mindegyik szál ugyanazt a kódot futtatja, csak eltérhet, hogy melyik elágazásba melyik azonosítójú szálat engedjük be.
-
Adatok elosztása
Dedikált adatokat, vagy egy közös tároló logikai résztömbjét érik el a szálak. Fontos eleme az SMPD mintának, környezettől függően más-más implementációt jelent. Gyakori adatelérés esetén érdemes az adatot a szál lokális memóriájába másolni, hogy kevesebb kommunikációra legyen szükség.
-
Befejezés
A szálak leállítása, vagy bevárása, ha szükséges akkor az eredmények összegyűjtése (globális tárolóba vagy egyik szál lokális memóriájába). Ha olyan a feladat, akkor szükséges lehet egy randevú jellegű szinkronizációs pont létrehozása.
Tulajdonságok
- Fontos az adatok elosztása
- Számolni kell ennek az adatok dekompozíciójának, másolásának költségével (overhead)
- A lokális memóriába másolás így is megérheti, mert kisebb az overhead, mint hálózati kommunikációval
- Előnyök:
- könnyen áttekinthető a közös kódbázis miatt
- overhead csak az indítás, inicializálás és befejezés szakaszban fordulhat elő
Tipikus használati esetek
Jól használható, ha teljesülnek az alábbiak:
- feladatpárhuzamosság,
- a feladatok között nincs összefüggés,
- kommunikációra nincs szükség a szálak között.
Jó hatásfok érhető el geometriai felbontás esetén, ha a problémateret diszkrét alterekre bontjuk, és az ezeken végzett műveleteket külön műveletvégzőkhöz rendeljük: a feladatok ebben az esetben azonosak vagy hasonlóak, míg a szálak közti interakció úgyszintén nem jellemző.
Loop Parallelism
A Loop Parallelism mintát akkor használjuk, ha
- a megoldandó feladatban feladatpárhuzamosság alakítható ki
- középpontjában nagy lépésszámú ciklusok állnak
- a környezet pedig egy közös memóriájú rendszer
Elosztott rendszer esetében a Master/Worker vagy az SMPD minta használható a ciklus feldarabolására.
A minta előnye, hogy nem kell nagyon átalakítani az algoritmust, nem is kell érteni az egészet, csak a számításintenzív ciklust kell azonosítani és függetleníteni az iterációkat.
A minta alkalmazásának lépései
-
Számításigényes ciklusok felfedezése
Kód analízise, mérések készítése. Ha a bottleneck egy ciklus, jöhet a következő lépés.
-
Cikluson belüli függőségek megszüntetése
- A különböző iterációkat párhuzamosan feldolgozható, (részben) független feladatokká próbáljuk alakítani.
- Teljesen nem mindig lehet, de a cél a minél nagyobb függetlenség.
- Jellemzően a közös változókat szükséges elkerülni ideiglenes változók használatával, így a számítási komplexitást memóriaköltséggé alakítjuk.
-
Ciklusok párhuzamosítása
- A a kialakított feladatokat hozzárendeljük az elérhető műveletvégzőkhöz
- Ciklusváltozók tartományának felbontása
-
Ütemezés optimalizálása
- A feladatok vélhetően hasonlóak, a komplexitásuk is vélhetően hasonló
- ha mégsem, a programozó feladata figyelni a terheléseloszlásra
- A feladatok vélhetően hasonlóak, a komplexitásuk is vélhetően hasonló
8. tétel - Párhuzamos tervezési minták II.
Mutassa be a Master/Worker tervezési mintát! Ismertesse a tulajdonságait, az általános felépítését, valamint tipikus használati eseteit! Mutassa be a Fork/Join tervezési mintát!
Master/Worker
A Master/Worker minta azokban az esetekben használható hatékonyan, amikor a terheléselosztás nehezen valósítható meg a szálak között és ezért nem célszerű előre műveletvégzőket rendelni adott feladatokhoz.
Akkor is megoldást nyújthat, ha a logika intenzív része nem számlálós ciklusba rendezett, mérete nem ismert előre, és nem is becsülhető meg.
Tehát akkor jó, amikor:
- nagy mennyiségű, nem összefüggő adatunk van
- jó terheléseloszlás mellett szeretnénk elvégezni a feladatokat
Általános felépítése
flowchart TB
MI[Master Inicializál] --> WI & W2 & W3 & W4
subgraph W1[W1: worker életciklus]
WI[Inicializálás] --> WF[Feladat kérése a Mastertől] --> WV[Feladat végrehajtása] --> COND{Van még megoldatlan feladat?}
COND -->|Van| WF
COND -->|Nincs| WL[Leállás]
end
subgraph W2
end
subgraph W3
end
subgraph W4
end
WL & W2 & W3 & W4 --> MB[Master begyűjti az eredményeket] --> ML[Master leáll]
-
Master inicializál
- Betölti a problémát
- deklarálja a részproblémák tárolására alkalmas szerkezetet,
- betölti a részfeladatokat,
- majd indítja a Worker elemeket.
-
Worker életciklus
a) Inicializálás
b) Feladat kérése a Mastertől
c) Végrehajtás
d) Ha van még megoldatlan feladat, akkor ugrás a b) pontra
e) Kilépés -
Master begyűjti és összegzi az eredményeket
-
Leállítás
Tulajdonságok
- A feladatokat tartalmazó adatszerkezet (bag of tasks) jellemzően egy szálbiztos sor
- A feladatok nincsenek statikusan hozzárendelve a műveletvégzőkhöz
- A terheléselosztás automatikus (egy szál új feladatot kap, ha végzett az előzővel)
- Jól skálázható: ha a feladatok száma jóval nagyobb a műveletvégzők számánál, a párhuzamos gyorsítás közel lineáris
- A Master a feladatok legyártása után Workerré válhat
- Átalakítások:
- Work stealing: a workereknek saját munkasora van, és lophatnak egymáséról ha kifogytak
- Hibatolerálás megoldható, ha ugyanazt a feladatot több workernek is kiosztjuk
- Hátrány:
- kihívás lehet a befejezés detektálása
- pl. ha a Master már a gyártás közben indítja a workereket, szükség lehet egy logikai változóra is, a sor ürességének ténye nem elég
- poison pill: speciális feladat, ami azt jelzi, hogy nincs már feladat, és leállhat a worker
- ha a szálaknak a műveletvégzés során kommunikálni kell egymással, vagy a feladatok között függés van, akkor ez a minta nem alkalmazható.
- kihívás lehet a befejezés detektálása
Fork/Join
Abban az esetben használjuk a Fork/Join mintát, ha a részproblémák létrehozása dinamikus, a bemeneti paraméter függvénye. Ekkor nem ismert előre a részfeladatok száma.
Tipikus használati esete az „oszd meg és uralkodj” elvű problémák, amikor a feladatot addig bontjuk részproblémákra, amíg el nem érünk az alapesetig, majd visszafelé felépítjük a megoldást.
A minta neve a szálak elágazáskori létrejöttéről (fork), és később a szinkronizációkor való visszacsatlakozásról (join) kapta.
Az implementációkor a fő problémát a szálak létrehozásából, menedzsmentjéből és megszüntetéséből adódó overhead okozza, amellyet kétféle leképezéssel oldhatunk meg.
A direkt leképezés során a szálak és a részprobléma létrehozása egyszerre történik. A forráskódban, ahol szükséges, létrejön a szál, a szülő szál pedig blokkol, amíg a gyermek nem végzett a feladatával. Tehát a program egy szállal indul, amelyről egyre több szál ágazik le, és várakozik ezek befejeződésére. A gyermek szálakból további szálak ágazhatnak le.
Az indirekt leképezés az előbb kialakuló jelentős overheadet hívatott csökkenteni. A direkt lekézesés során a szálak létrehozása a teljes végrehajtást lassítja, illetve ronthatja a hatékonyságot. Szálak létrehozása és megszüntetése helyett használható az úgynevezett thread pool, amikor a program indításakor újrahasznosítható szálak jönnek létre, feladatuk befejeztével pedig visszakerülnek a poolba. Ezzel a szerkezettel a feladatokhoz nem kapcsolódnak dedikált szálak, tehát csökken a létrehozásból, ütemezésből és megszüntetésből adódó overhead.
A minta szorosan kapcsolódik a Loop Parallelism és a Master/Worker mintához is.
9. tétel - Parallel sum & prefix scan
Mutassa be a párhuzamos összegzés módszereit! Mely esetekben használható a redukció? Hogyan párhuzamosítható a részösszegek számítása? Ismertesse a prefix scan algoritmusát!
Redukció
- Képzeljünk el egy feje tetejére állított bináris fát
- Pontosan annyi levéleleme van, mint ahány összegzendő elemünk
- Ha a közbülső elemek értékét a gyermekelemeik összegében határozzuk meg, akkor a gyökérelembe kerül az összeg
- Így az összegzés \(logN\) darab konkurens lépésben megoldható, míg szekvenciálisan \(O(n)\) komplexitású lett volna
- Szinkronizációs pontok szükségesek: az előző szint részeredményeit be kell várni, hogy a következő szint megoldását megkezdjük
- A részeredményeket tárolhatjuk külön, vagy felülírhatjuk a tömb elemeit, ha ez nem gond
- Ha a tömb elemszáma (
n) páratlan, akkor a szélső eseteket külön kell vizsgálni
Lépések

Megvalósítás

Megvalósítás vizualizálása

Adatdekompozíciós módszer
- A redukció akkor hatékony, ha szintenként az egyes konkurens műveletekhez dedikált műveletvégző párosul
- ehhez 8 elemnél 4 műveletvégző kell, ami jelentős ilyen kevés elemre
- ezt oldja meg az adatdekompozíció módszere
- Durvább szemcsézettségű megoldás, mint a redukció
- Nagyobb blokkokat határozunk meg
- A résztömböket dolgozzuk fel párhuzamosan
- A szálak számának meghatározása történhet az elérhető műveletvégzők száma alapján

Megvalósítás
t: a szálak száma
i: a szál azonosítószáma
feltételezzük, hogy a tömb mérete osztható a szálak számával
sumtömb t elemből áll, melyek kezdeti értéke 0- Minden szálnak van egy dedikált eleme a
sumtömbben, ebbe összegzi a saját résztömbjét - Miután minden szál végzett, a
sumtömb elemeinek összege adja az összes elem összegét.

Prefix Scan
- Részösszegek számítására szolgáló módszer
- Bemenete: n elemű tömb
- Kimenete: n elemű tömb, ahol a tömb i. elemében az elemek összege van, az első elemtől az i.-ig
- inkluzív prefix scan: az összegbe beleszámoljuk az i. elemet is
- exkluzív prefix scan: az i. elem nem számít bele
- A prefix scan szekvenciálisan is implementálható, de ekkor a komplexitása O(n).

Párhuzamos megvalósítás


Ha részletes magyarázatra van szükséged az algoritmus lépéseiről, itt találod a jegyzetben.
Adatdekompozíción alapuló megvalósítás
- A párhuzamos prefix scan is sok műveletvégzőt igényel, így itt is érdemes lehet adatdekompozícióval próbálkozni

- Az eredeti tömb geometriai dekompozíciója, a műveletvégzők számához igazodó darabszámú résztömb létrehozása
- A szétdarabolt tömb elemein helyi inkluzív prefix scan futtatása
- Miután a helyi műveletek véget értek, a prefix scan által előállt eredménytömbök utolsó elemeit (résztömbök összegeit) külön munkatömbbe gyűjtjük
- Ezen elemek exkluzív prefix scanjét kiszámoljuk
- A második lépésben előállt résztömbök elemeit a negyedik pontban kiszámolt tömbben tárolt értékekkel megnöveljük
- Ezáltal előáll az eredeti tömb inkluzív prefix scanje.
10. tétel - Párhuzamos rendezés
Milyen módon párhuzamosítható a buborékrendezés? Ismertesse a páros-páratlan felbontás elvi alapjait! Mutassa be az oszd meg és uralkodj elvű megoldásokat párhuzamos rendezésre!
Buborékrendezés párhuzamosítása
Szekvenciális buborékrendezés
- működése két egymásba ágyazott cikluson alapul, amelyek hatásaként páronként összehasonlításra kerülnek az egymás melletti elemek, és szükség esetén csere történik
- N-1 darab fázis van
- az első fázisban N-1 összehasonlítás, aztán mindegyik fázisban eggyel kevesebb
- az első fázisban a tömb utolsó eleme kerül a helyére, a következőben az utolsó előtti, és így tovább
- Az összehasonlítások száma összesen \( \frac{N(N−1)}{2} \), a futásidő \(O(N^2)\)

Párhuzamosítás
Futószalag elvű
- Az első fázis elindulásakor az első két elem kerül összehasonlításra és esetleg cserére, ezt követően a 2. és 3. elemek. Amikor a 3. és 4. elemekre kerül a sor, akkor a második fázis indítható az első és második elemek feldolgozásával, hisz az első fázis a továbbiakban nem érinti ezeket, és így tovább.
- Működőképes, de
- szinkronizálni kell a feldolgozást, mert el kell kerülni a versenyhelyzetet
- a később indult fázis ne tudjon a következő elempárra lépni, amíg a korábban indult azokat még nem dolgozta fel
- nem hatékony: a műveletvégzők száma nem azonos végig
- kezdetben 1
- legfeljebb \(\frac{1}{2}\)-re növekszik
- majd az utolsó fázisoknál ismét lecsökken
- szinkronizálni kell a feldolgozást, mert el kell kerülni a versenyhelyzetet

Páros-páratlan felbontás elvi alapjai
- hatékonyabb, mint a futószalagos megoldás
- összesen \(N\) darab konkurens lépés történik, melyek között megkülönböztetünk páros és páratlan fázisokat
- páros fázis: a páros sorszámú elemek kerülnek összehasonlításra (és cserére) a jobb oldali szomszédjukkal;
- páratlan fázis: a páratlan sorszámú elemek kerülnek összehasonlításra (és cserére) a jobb oldali szomszédjukkal
- így összesen \(\Bigl\lceil \frac{N}{2} \Bigr\rceil\) db, egy páros és egy páratlan fázisból álló iteráció kell csak a rendezéshez
- ezáltal a szükséges műveletvégzők száma \(\Bigl\lfloor \frac{N}{2} \Bigr\rfloor\)
- előny: műveletvégzők kihasználtsága jó
- hátrány: overheadet okoz az elemek konkurens elérésének biztosítása

Oszd meg és uralkodj elvű megoldások párhuzamos rendezésre
Összefésülő rendezés
- a tömb előbb megfelezésre kerül, majd az előállított résztömb további felezésével egyre kisebb részfeladatokra bomlik
- amikor a résztömbök már csak 1 elemet tartalmaznak, akkor a szomszédos blokkok összefésüléssel egyesülnek
- A szekvenciális futásidő \(O(N \log N)\) függvényében adható meg
Párhuzamosítás
- Két szakasz:
- felbontás: \(\lceil \log N \rceil\) lépés
- egyesítés: \(\lceil \log N \rceil\) lépés
- Fork/Join mintán alapul
- szintenként lefelé haladva különböző, egyre nagyobb
elemszámú tömbök összefésülése szükséges
- a műveletek száma, időigénye különböző

Gyorsrendezés
- egy támpontnak (pivot) nevezett elem szerint kerül felbontásra a tömb
- E támpont elem elé mozgatjuk a kisebb, mögé pedig a nagyobb
elemeket
- a támpont elem a végleges helyére kerül
- a két résztömb pedig függetlenül rendezhető
- Ha a résztömb nem egységnyi méretű, akkor ismét szétválogatás, majd felbontás következik.
- a támpont választás befolyásolja a futásidőt
- átlagban \(O(N \log N)\)
- rossz esetben \(O(N^2)\)
- szintén Fork/Join minta

(A támpont elem ebben a példában mindig a tömb vagy résztömb első eleme.)
11. tétel - Optimalizálás alapfogalmai
Mit értünk optimalizálási feladat alatt? Ismertesse az optimalizálás alapvető fogalmait (célfüggvény, megszorítás, fitnesz,keresési/probléma tér, optimum, genotípus, fenotípus)! Mutasson gyakorlati példákat ezekre! Milyen módon lehet csoportosítani az optimalizálási módszereket?
Optimalizálási feladat
- Olyan feladat, melynek célja, hogy valamilyen problémára megtalálja az optimális megoldást.
- Lehetnek
- matematikai hátterűek (pl. függvény minimumának megkeresése)
- való világból érkező gyakorlati problémák (pl. az optimális termeléi ütemezés meghatározása)
- természetiek (pl. evolúció is egy optimalizálás)
- Informatikai szempontból az optimalizálást általában egy vagy több függvény minimumának megkereséseként értelmezzük, erre sok gyakorlatorientált probléma visszavezethető.
Fogalmak
1. Problématér (\(ℙ\))
Egy halmaz, ami tartalmazza a feladat megoldásjelöltjeit (összes lehetséges megoldás)
Például:
- függvényközelítés esetén: elemei a lehetséges függvényparaméterek
- utazó ügynöknél: lehetséges útvonalak
2. Célfüggvény (\( g: ℙ → ℝ\))
- Az optimalizálás során számszerűsítenünk kell a problématérban található megoldások jóságát.
- A célfüggvény minden problématérbeli elemhez egy számot rendel.
Például:
- függvényközelítésnél: a referenciafüggvény és a megoldásjelölt függvény különbsége
- utazó ügynöknél: a városok adott permutációjához tartozó útvonal hossza
3. Globális optimum:
A problématér azon elemei, amelyeknél nincs "jobb" elem. Általában a legkisebb értéket keressük, de fordítva is lehet.
Például:
- utazó ügynöknél: a legrövidebb útvonalak
4. Lokális optimum:
A problématér azon elemei, amelyeknél egy adott környezetben nincs "jobb" elem. Általában a legkisebb értéket keressük, de fordítva is lehet.
Fontos, hogy ez nem "majdnem jó" érték. Lehet nagyon messze van a megoldástól, csak a problématér olyan részén van, ahol a környezetében nincsen nála jobb elem.
5. Megszorítások:
Gyakran van, hogy a leendő megoldásoknak különféle megszorításoknak is meg kell felelniük, amikből több lehet.
Például: gyártási folyamat tervezése → egyik műveletnek meg kell előznie a másikat
A megszorításokat függvényekként értelmezzük, halmazukat \(ℂ\)-vel jelöljük. Egy megoldásjelölt akkor elégít ki egy megszorítást, ha a függvény értéke a megoldásjelöltre legalább 0.
\[ \forall c \in ℂ: c(x) \geq 0 \]
6. Keresési tér (\(𝕊\))
- A problématérből kell választani megoldásjelölteket
- Ezek közül egyet vagy többet kiválasztunk
- Az optimalizáló algoritmusunk ebben fog működni
- Miben más, mint a problématér?
- Más szerkezetű
- Pl. utazú ügynöknél a problématér az útvonalak, a keresési tér a városokat jelölő számok tömbje
- A problématér kisebb szelete
- Pl. ki tudjuk zárni a reménytelen megoldásjelölteket
- A problématér leegyszerűsítése
- Pl. a gyártási folyamat optimalizálásánál annak csak bizonyos részeivel foglalkozunk
- Más szerkezetű
Nem muszáj megkülönböztetni a problémateret és a keresési teret.
7. Fenotípus, Genotípus
A problématér és a keresési tér közötti leképezéshez használjuk ezeket.
- Fenotípus: a problématér elemei
- Genotípus: a keresési tér elemei
Genotype-phenotype mapping: függvény, ami a keresési térből a problématérbe képezi le az elemeket.
\[gpm: 𝕊 → ℙ \]
A leképezésnek legalább az egyik irányba teljeskörűnek kell lennie.
- Tehát a keresési tér összes eleméhez tudjunk rendelni elemet a problématérből.
8. Fitnesz függvény
A keresési térben értelmezett függvény, ami minden elemhez hozzárendel egy jóságot.
\[f: 𝕊 → ℝ\]
- Lehet a célfüggvény egyszerűsítése, vagy több célfüggvény összevonása.
- Tartalmazhatja a megszorításokat is.
- Felhasználható arra is, ha több megoldásból az egymástól legtávolabbiakat akarjuk választani
Összehasonlító táblázat
| Problématér | Keresési tér | |
|---|---|---|
| Jele | ℙ | 𝕊 |
| Elemeinek neve | fenotípus | genotípus |
| Jóságot jellemző függvény | célfüggvény (\(g\)) | fitnesz függvény (\(f\)) |
Optimalizálási módszerek csoportosítása
flowchart TB O["`**Optimalizálási módszerek**`"] A["`**Analitikus módszerek** *(matematikai eszközökkel levezethető megoldások)* `"] N["`**Numerikus módszerek** *(lineáris programozás, nemlineáris programozás, dinamikus programozás, visszalépéses keresés, stb.)*`"] H["`**Heurisztikus módszerek** *(hegymászó módszer, genetikus algoritmusok, raj alapú módszerek, stb.)* `"] O --> A & N & H
12. tétel - Többcélú optimalizálás
Mit értünk többcélú optimalizálás alatt? Mik ezeknek a feladatoknak a jellegzetességei és nehézségei? Milyen módon lehet visszavezeti ezeket a feladatokat egycélú optimalizálásra? Ismertesse a Pareto dominanciával kapcsolatos fogalmakat (dominancia, Pareto optimum, Pareto front)! Mutasson gyakorlati példát ezekre!
A valóságban sok olyan optimalizálási probléma létezik, ahol nem tudunk egyetlen egyértelmű célfüggvényt definiálni.
Például:
- befektetést kell ajánlani, minél nagyobb hozammal, de minél kisebb kockázattal
- munkát szeretnénk elvégeztetni, minél jobb minőségben és minél olcsóbban
Ilyenkor több célfüggvény van, és \(G\) a célfüggvények halmaza.
Egy célfüggvényt felírhatunk, mint
\[g_i: ℙ → ℝ, i \in \lbrace 1,2,...|G| \rbrace\]
Visszavezetés egycélú optimalizálásra
A legtöbb általunk használt algoritmus egycélú optimalizálásra van, többcélúra közvetlenül nem használható, de ezeket különböző módszerekkel egycélú optimalizálásra vezethetjük vissza.
flowchart TB V[Visszavezetés egycélú optimalizálásra] --> O & MD & MM & H O[Összegzés] --> S[Súlyozás] MD[Method of Distance] MM[Min-Max] H[Hierarchikus módszer]
Összegzés, súlyozás
- Legegyszerűbb, ha a fitneszfüggvényt úgy valósítjuk meg, hogy a célfüggvényeket összeadjuk
- Ennél nem sokkal bonyolultabb, ha az öszegzés során súlyvektorral súlyozzuk a célfüggvényeket.
- Előny:
- egyszerűség: a kapott fitnesz függvényt simán felhasználhatjuk a tanult algoritmusokban
- a súlyokkal beállítható a célfüggvények fontossága
- Hátrány:
- nehéz lehet meghatározni a súlyokat
- bizonyos esetek nem írhatóak le súlyozással
- pl. befektetésnél van akkora kockázat, ami bármekkora is lehet a hozam, nem éri meg
Method of Distance
- Meghatározzuk célértékek egy vektorát (ideális pont)
- lehet akár mindegyik koordináta 0
- Egy elem jósága a hozzá tartozó célfüggvények értékei által megjelölt pont távolsága ettől az ideális ponttól
- Pl. van egy adott hely, ahova szeretnénk egy bútort venni
- Az ideális bútor 100 cm magas, 50cm széles és 40 cm mély
- Ekkor a célfüggvények:
magasság(),szélesség(),mélység() - Ekkor a célvektor: [100, 50, 40]
Képlet:
\[ (\sum_{i=1}^{|G|} |g_i(gpm(x))- \hat{v}_i|^r)^{\frac{1}{r}} \]
\(r\) segítségével lehet beállítani a távolságszámítás módszerét, pl. \(r=2\) esetén a távolság Euklideszi lesz.
Min-max
- Figyelembe tudja venni az egyes célfüggvények értékkészlete közötti különbségeket
- pl a kockázat 0 és 1 közötti számként, a hozam meg 0 és 1 000 000 000 számként van megadva
- Szintén definiálunk egy vektort (ideális pont)
- Az egyes célfüggvényeket normalizáljuk:
\[ Z_i(x) = \frac{|g_i(gpm(x))-\hat{v}_i|}{\hat{v}_i} \]
Ezek a \(Z\) értékek tehát az egyes célokra vonatkoznak, még valamilyen formában összegeznünk kell őket a fitnesz függvény megadásához.
- lehet sima összegzés
- választhatjuk a legrosszabb eredményt
Hierarchikus módszer
- A célfüggvényeket sorrendbe rakjuk fontosság szerint.
- Két elem összehasonlításánál először kiértékeljük az elsőt, ha azonos az eredmény akkor a másodikat, és így tovább
- Például egy versenyen ha két ember azonos pontot ér el, a nevük ABC sorrendje dönt
- Hátrány:
- későbbre priorizált célfüggvény csak a saját szintjén tudja befolyásolni a sorrendet
- nem ad egyértelmű értéket a fitnesznek, csak két elem összehasonlításakor tudja megmondani, hogy melyik a jobb
Pareto dominancia
Egy \(x\) megoldás Pareto dominál egy \(y\) megoldást, ha
\[\forall i \in \lbrace 1,2,...,|G|\rbrace: g_i(x) \leq g_i(y)\]
\[\exists j \in \lbrace 1,2,...,|G|\rbrace: g_j(x) < g_j(y)\]
Tehát
- \(x\) minden szempontból legalább olyan jó, mint \(y\)
- és legalább egy szempontból még jobb is nála
Jelölése: \[x \prec y\]
Pareto optimum
Egy megoldásjelölt Pareto optimum, ha nincs olyan megoldásjelölt, ami dominálná őt.
- Pl. ha a állásajánlatoknál a fizetést és a home office napok számát vesszük, akkor ha van egy olyan ajánlat, amelyik a legtöbbet fizeti és full remote, az pareto optimum lesz
Pareto front
A Pareto optimális elemek halmaza (ha több van).
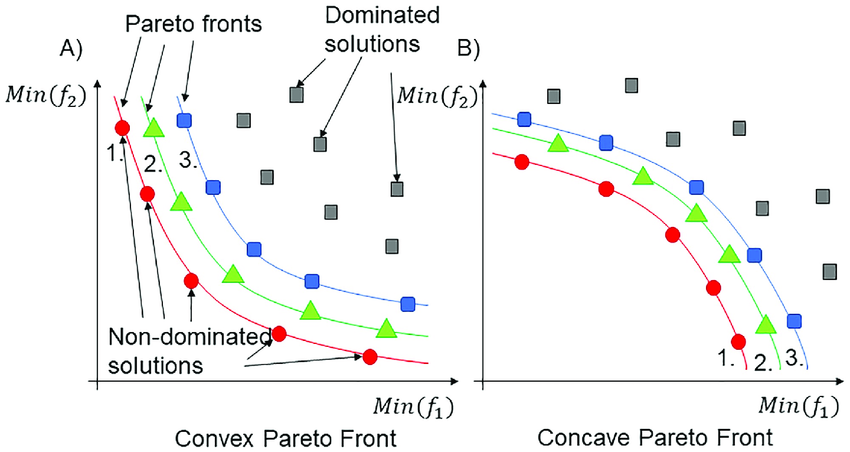
Több front is lehet.
- A második pareto frontba azok az elemek tartoznak, amiket csak az első pareto front elemei dominálnak.
- A harmadikba azok, amiket az első két pareto front elemei dominálnak
- és így tovább.
13. tétel - Lokális optimalizálás
Mit értünk lokális optimalizálási módszerek alatt? Mutassa be a hegymászó módszert és annak variánsait (sztochasztikus, steepest ascent)! Ismertesse a Tabu keresés algoritmusát!
Hegymászó módszer
- kiválasztja a keresési tér egy véletlen pontját
- egy ciklust futtat, ami ezt a pozíciót tudja megváltoztatni, hogy jobb helyre jussunk
- ha sikerül: ez lesz az új pozíció, a ciklus folytatódik
- ha nem sikerül: tovább próbálkozik vagy leáll
- egyik legrégebbi, legegyszerűbb módszer
- már meglévő kereséseket is lehet vele finomhangolni
- az elnevezés megtévesztő, a legkisebb fitnesz felé akarunk haladni, nem a legnagyobb felé
A megvalósítások abban különböznek, hogy hogyan vizsgálják az aktuális pont környezetét.
Sztochasztikus hegymászó

flowchart LR
RAND[Véletlen pont kiválasztása]
STOPCOND{Leállási feltétel igaz?}
SEARCH[Véletlen pont választása ϵ távolságra]
ISBETTER{Jobb az új pont?}
STEP[Lépés az új pontba]
STOP["`Leállás, vissza *gpm(p)*`"]
STOPCOND-- nem -->SEARCH-->ISBETTER--nem-->STOPCOND
ISBETTER--igen-->STEP-->STOPCOND
RAND --> STOPCOND-- igen -->STOP
-
Az algoritmus kiindul egy véletlen pozícióból
-
Egy ciklust futtat addig, amíg a leállási feltétel nem lesz igaz
A leállási feltétel lehet pl:
- időkorlát,
- fitnesz korlát,
- fitnesz javulás korlát
-
Az aktuális pozíciót
pváltozó tárolja. A cikluson belül választ egy véletlen pozíciót (q) ennek \(ϵ\) sugarú környezetében.- Ha az új pont jobb, akkor átlép ide
- Ha nem, akkor tovább próbálkozik
-
Az algoritmus visszatérési értéke a
páltal reprezentált megoldás
Megjegyzések
- Indeterminisztikus módszer (minden indításkor más lehet a pont, de azonos pontból indulva is más lehet az eredmény)
- Fitnesz vizsgálatnál "\(<\)" helyett "\(\leq\)" használatával a síkságokon is továbblép
- \(ϵ\) értéke változtatható, pl. megakadásnál
Steepest Ascent

A q elemet ebben nem véletlenszerűen választjuk, hanem az \(ϵ\) sugarú környezet legjobb eleme lesz kiválasztva.
Fel tudja ismerni, ha globális oprimumba ragad: a sztochasztikus változat abban az esetben, ha a q pont nem volt jobb, mint p, akkor egy újabb véletlen szomszéd felé próbálkozott. Ebben a verzióban ennek nincsen értelme már, mert q biztosan a legjobb a szomszédok közül, a keresés akár le is állítható.
Megjegyzések
- Ez már determinisztikus (azonos helyről indulva: ugyanaz az út, ugyanaz a megoldás)
- A gyakorlatban általában nem kivitelezhető a környezet legjobb elemét kiválasztani
- 1 dimenzióban csak két elem van \(ϵ\) távolságra, 2 vagy több dimenzióban már végtelen
- így a környezetet általában valamilyen felbontással vizsgáljuk meg
- Kevesebb lépést tesz meg, de sokkal számításigényesebb a környezet vizsgálata
- Tehát a teljes algoritmus futásidejére nem várhatjuk, hogy jobb legyen
Tabu keresés
- A hegymászó egyik hiánya, hogy könnyen beragad a lokális optimumokba
- Felmerül az ötlet, hogy többször kéne elindítani más kiindulópontokkal
- A keresések függetlenek, így belefuthatnak ugyanazokba az utakba, ahol várhatóan ugyanahhoz a végeredményhez jutnak
- Érdemes lenne eltárolni a már megtett utakkal kapcsolatos tudást
- Minden lépést eltárolni túl memóriaigényes lenne, és nehéz lenne benne keresni
A hegymászót úgy módosítjuk, hogy tabu ponthoz érve hagyja abba a belső ciklus futtatását.

Segédfüggvények
-
SetTabuBarrier():- elhelyez egy jelzést a tabu pontok listájába, ami azt jelzi, hogy az ezt követő pontok az aktuális kereséshez tartoznak
- így a keresés nem akad össze a saját pontjaival
-
IsTabu(p): keres a tabu tárhelyen, ésigaz-at ad vissza, ha a paraméterben megadott pozíció tabu -
AddTabu(): felvesz egy új elemet a tabu tárhelyre -
PurgeTabu(): tömöríti a tabu tárhelyet
Megjegyzések
- Nem feltétel, de itt a steepest ascentet használtuk, mert determinisztikus
- ekkor nyilvánvaló a tabu szerepe, mert egy pontból mindig ugyanoda jut
- A kereséskor érdemes a pont környezetét keresni a tabu tárhelyen, mert többdimenziós feladatnál kicsi az esélye, hogy az algoritmus többször lép pont ugyanabba a pontba
Tabu tárhely kezelése
- Tárolás
- Végtelen lista
- Hasító táblák: gyors, de csak teljes egyezésre keres
- Tulajdonságok tárolása: nem a pontot, hanem valamilyen tulajdonságát tároljuk
- Változások tárolása: nem a megoldásjelölteket, hanem az azok közötti változásokat tároljuk
- Keresés
- Lineáris keresés
- Térbeli indexelés: a keresési tér részterekre bontásával, és a részterekben keresünk
- Karbantartás
- FIFO lista: korlátozzuk a tárolt elemek számát, új elem érkezésekor a legrégebbit töröljük, ha tele van
- nem szerencsés, attól hogy régi még lehet hasznos
- Klaszterezés: az egymáshoz közeli pontokból úgy törlünk, hogy a lefedett terület ne változzon
- FIFO lista: korlátozzuk a tárolt elemek számát, új elem érkezésekor a legrégebbit töröljük, ha tele van
Értékelés
- Többszöri újraindításra jelentősen csökkentheti a futásidőt
- Főleg determinisztikus kereséseknél hatékony
- Nem csak hegymászónál használható, más heurisztikák is kiegészíthetőek vele
- Hátrányok:
- Csak kis méretű keresési térnél működik hatékonyan
- A keresés lépés időigényes
14. tétel - Véletlen módszerek
Mutassa be a véletlen optimalizálás módszerét! Miben különbözik ez a lokális optimalizálástól? Ismertesse a szimulált lehűtés algoritmusát! Milyen paraméterei vannak ennek? Mik az előnyei a hegymászó módszerekhez képest?
Véletlen optimalizálás
- A hegymászó módszer egyes hátrányaira próbál megoldást nyújtani
- Többdimenziós keresésnél a hegymászó általában egy időben csak egy paraméter értékét változtatja
- A hegymászónál rögzített a lépési távolság (\(ϵ\))
- A hegymászó könnyen beragad a lokális optimumokba
- Az alapelve megegyezik a hegymászónál tanulttal:
- egy elemet vizsgál
- egy véletlen pontból indul
- minden lépésnél próbál jobb fitneszű pozícióba kerülni
Megvalósítás

- véletlen pontból indítjuk
pváltozót - megállapítjuk a továbblépés irányát
- több dimenziós tér esetén minden dimenzióban lépünk
- nem fix távolságot lépünk, hanem ezt egy \((\mu, σ)\) paraméterű normál eloszlással határozzuk meg
- a
ppozícióhoz hozzáadjuk a kiszámított irányvektort, az így kapott pontot hasonlítjuk össze az aktuális ponttal - ha jobb, akkor átlépünk, különben nem
- a peremfeltételeket is vizsgáljuk, ha azoknak nem felel meg, akkor sem lépünk át
Megjegyzések
- A
µértékek a haladási irányt befolyásolják (pozitív vagy negatív)- jellemzően \(\mu=0\) egy kiegyensúlyozott érték
- A
σértékek a véletlen számok méretét befolyásolják- általában kicsi, hogy a szomszédságot tudjuk vizsgálni
- A normál eloszlás nem korlátos, így mindig lesz esély nagyot lépni negatív/pozitív irányba
- ezáltal ki tud lépni a lokális optimumokból
Véletlen optimalizálás vs. lokális optimalizálás
Különbségek a hegymászóval szemben:
- Nem csak a tengelyek iránti elmozdulást figyeli
- A lépés mérete nem fix, hanem egy eloszlás alapján határozzuk meg
- Rendelkezik a hegymászó előnyeivel
- Nagyobb eséllyel lép ki a lokális optimumokból
- Elvben mindig megtalálja a globális optimumot (végtelen idő alatt)
További tulajdonságok
- Nem determinisztikus módszer
- Csak \(ℝ^N\) keresési térben használható
Szimulált lehűtés
- A hegymászó továbbfejlesztésének tekinthető
- A hegymászó könnyen beleragad a lokális optimumokba, és csak konvex problémáknál ad garantáltan helyes megoldást
- Alapelve a kohászatból származik: az anyagok minősége jelentősen javítható egy vagy több melegítést és lehűtést végrehajtva
- lassú lehűtés => jobb eredmény (globális optimum)
- gyors lehűtés => kevésbé jó eredmény (lokális optimum)
- Nem kényszerítjük a rendszert túl gyors konvergenciára, mert úgy lokális optimumban ragadhat.
- Lassabb konvergenciát próbálunk elérni
- eleinte engedjük a negatív irányú lépéseket is
- a későbbiekben csökkentjük ennek a szerepét.
- eleinte engedjük a negatív irányú lépéseket is

- elindul egy véletlen pontból
- innen próbál jobb és jobb helyre átlépni
- közben figyeli a megállási feltételt
- a lényeges különbség a hegymászóhoz képest a fitnesz ellenőrzése
- ha jobb a fitnesz: átlép
- ha rosszabb: egy bizonyos valószínűséggel ekkor is átlép
- kiszámolja a hőmérsékletet (
T) - a valószínűség a annál nagyobb, minél nagyobb a
T
- kiszámolja a hőmérsékletet (
Tfolyamatosan csökken a szimuláció soránpértéke nem mindig a legjobb talált elemet tárolja, ezért azt külön kell tárolni egypoptváltozóban.
Paraméterei
-
T:- minél nagyobb, annál megengedőbbek vagyunk a kedvezőtlen változások felé
- 0 nem lehet az osztás miatt, de ahhoz közeli értékeknél már szinte hegymászóként viselkedik az algoritmus
-
kB:
- Boltzmann állandóra utal, tetszőlegesen beállítható konstans
- minél nagyobb, annál megengedőbb a rendszer
∆E: minél nagyobb, annál kisebb az esély az elfogadásra
Hőmérséklet meghatározása
flowchart TB H["Hőmérséklet-meghatározási módok"] IK[Időkorlátos] IL[Idővel lassulva csökkenő] F[Fitneszfüggő] H --> IK & IL & F
-
Időkorlátos esetben: \( Temperature(t) = T_{max} \cdot (1-\frac{t}{t_{max}})^{\alpha}\)
- \(\alpha\) értékével befolyásolható a hőmérsékletet leíró görbe
-
Idővel lassulva csökkenő: \( Temperature(t+1) = Temperature(t) \cdot (1- \epsilon)\)
-
Fitneszfüggő: \(Temperature = max(\beta \cdot (f(p_{opt})-f(p)), \gamma)\)
- a globális optimumhoz közeledve (egyre kisebb fitnesz) egyre szigorúbb a konvergencia
- \(\beta\) értéke kísérletekkel beállított konstans
- \(\gamma\) szerepe csak a nullás hőmérséklet értékének elkerülése (\(\gamma > 0\))
A hegymászó módszerhez képest
- Rendelkezik a hegymászó előnyeivel (egyszerű, hatékony, stb.)
Előnyei
- Ki tud ugrani a lokális optimumokból
- Megfelelően választott hűtési karakterisztika esetén biztosan megtalálja a globális optimumot
Hátrányai
- lépésszáma nagyobb lehet
- futásideje kedvezőtlenebb
- több paramétert igényel
15. tétel - Genetikus algoritmus I.
Mutassa be az evolúciós módszerek jellegzetességeit és alapvető lépéseit! Részletesen ismertesse a reprezentációs lehetőségeket (kromoszóma, populáció jellemzők)! Milyen fitnesz hozzárendelési módokat ismerünk (egyszerű fitnesz, rangsor, verseny)? Mik a kombinatorikai feladatok specialitásai?
Evolúciós módszerek jellegzetességei
- Alapelvüket a természetes szelekcióból (evolúció) merítik.
- Alapvető mechanizmusai:
- természetes kiválasztás: a jobb képességű elemek
- nagyobb eséllyel maradnak életben
- nagyobb eséllyel szaporodnak
- keresztezés: az új egyedek a kiválasztott szülők tulajdonságait öröklik valamilyen kombinációban
- mutáció: a leszármazottak nem mindig öröklik teljes egészében a szülők tulajdonságait, a tulajdonságaik bizonyos valószínűséggel véletlenszerűen megváltoznak
- legjobbak túlélése: a legjobb elemek jó eséllyel túlélnek
- természetes kiválasztás: a jobb képességű elemek
- A keresési tér (\(𝕊\)) tartalmazza a megoldásjelölteket, amiket egyedeknek vagy kromoszómáknak nevezünk.
- Többdimenziós tér esetén több paraméter értékét keressük, ezek a gének.
- A módszer egyszerre több megoldásjelölttel dolgozik, ezeket nevezzük populációnak (\(P\)).
- A módszer egy véletlenszerű állapotból indul.
- Több iteráción keresztül finomítja az egyes egyedek paramétereit
- Leállításkor azt várjuk, hogy a populáció egyedei jó fitnesz értékű megoldásjelöltek legyenek
Evolúciós módszerek alapvető lépései

InitializePopulation(): létrehozza a véletlen populációtEvaluation(): kiértékeli a populáció minden egyedét az átadott fitnesz függvény alapján, és minden egyed kap egy p.fitness értéket a saját jóságával.- Kiválasztjuk a populáció legjobb fitneszű elemét, és eltároljuk egy
pbestváltozóban - Fő ciklus futtatása a megállási feltételig
- A kilépési feltétel után a legjobb egyed lesz a visszatérési érték
A fő ciklus felépítése
Selection(): leendő szülők kiválasztása (\(M\) halmazba)- általában megengedett, hogy egy egyed többször is belekerüljön
- Létrehozunk egy \(P'\) halmazt, ide fognak kerülni a szülőkkel generált gyermek egyedek
- A belső ciklus addig tölti a \(P'\) halmazt, amíg az el nem éri a szükséges elemszámot
- kiválaszt
kdarab szülőt az \(M\) halmazból (ktetszőlegesen beállítható) - ezekből lesz egy új egyed a
CrossOver()függvény meghívásával - a
Mutate()függvény meghívásával mutálódik az elem - elhelyezi az elemet a \(P'\) halmazban
- kiválaszt
Reinsertion(): \(P\) és \(P'\) valamilyen kombinálásával előáll az új \(P\) halmaz- Kiértékeljük az egyedeket, és kiválasztjuk a legjobbat
Folyamatábra
Folyamatábra
flowchart TB
IP[Populáció létrehozása] --> EV[Kiértékelés] --> BEST[Legjobb elem mentése] --> S
subgraph MAIN[Fő ciklus]
S[Szelekció M-be] --> CREATE_P
CREATE_P["P' létrehozása"] --> PARENTS
subgraph INNER["Belső ciklus: Populáció feltöltése"]
PARENTS[k darab szülő választása M-ből] --> CROSS[Keresztezés] --> MUT[Mutáció]
MUT --> ADD["Hozzáadás P'-hez"] -->ISFULL
ISFULL{"P' tele van?"}
ISFULL--"nem"-->PARENTS
end
ISFULL--"igen"-->REINS
REINS["`Új *P* populáció készítése *P* és *P'* halmazokból`"] --> MAIN_EV
MAIN_EV[Kiértékelés] --> MAIN_BEST[Legjobb elem mentése]
MAIN_BEST --> STOPCOND{Megállási feltétel teljesül?}
STOPCOND--"nem"-->S
end
STOPCOND--"igen"--> STOP["Leállás, legjobb elem vissza"]
Kromoszóma reprezentáció
flowchart TB KR["Kromoszóma reprezentáció"] J["Gén reprezentáció"] Geno["Genotípus jellegű"] Feno["Fenotípus jellegű"] Perm["Permutációs"] H[Kromoszóma hossza] FH[Fix hosszúságú] VH[Változó hosszúságú] KR --> J & H J --> Geno & Feno & Perm H --> FH & VH
Gén reprezentáció
Milyen formában szeretnénk a kromoszómák adatait tárolni?
- Genotípus jellegű tárolás: a kromoszómát egy bitsorozatként írjuk le
- legegyszerűbb a számértékek tárolása bináris formában
- de ennek van egy hátránya: az egymás melletti számok Haming-távolsága különböző, így egy bit megváltoztatása lehet kicsi vagy nagy változás is
- ezért jobb a Gray-kódolás, ahol a számok Haming távolsága 1.
- legegyszerűbb a számértékek tárolása bináris formában
- Fenotípus jellegű tárolás: a kromoszóma közvetlenül a megoldás adatait tartalmazza
- a kereső algoritmus feladata, hogy a vektor elemeinek lehetséges intervallumait figyelembe vegye
- Permutációs ábrázolás: az egyes gének itt nem függetlenek egymástól, hanem mindig egy adott készlet elemeit tartalmazzák különféle sorrendben
Milyen legyen a kromoszóma hossza?
- Fix hosszúságú: egyszerű, az egyedekkel végzett műveletek ugyanolyan hosszú egyedet fognak eredményezni
- Változó hosszúságú:
- pl. útkeresési problémánál nem tudjuk előre, hogy milyen hosszú utat keresünk
- keresztezésnél a szülő kromoszómák hossza eltérhet
- mutációnál változhat a kromoszóma hossza
Fitnesz-hozzárendelési módok
- Egyszerű fitnesz hozzárendelés:
- egy darab fitnesz függvény van, ami minden egyedhez tud rendelni egy számot
- a fitnesz érték jelentéssel bírhat, pl. két elem között nagy a fitnesz különbség => az egyik sokkal jobb mint a másik
- nem mindig használható
- Rangsor alapú:
- ha nem tudunk pontos értéket rendelni az elemekhez, de össze tudjuk őket hasonlítani
- a rendezettséget használjuk fitnesz értékként
- pl. pareto dominanciával is meg lehet adni a fitnesz értéket
- Verseny alapú:
- a rangsor alapú hozzárendelés számításigénye nagy, ehelyett használhatunk közelítő számításokat
- \(t\) szintű bináris verseny: minden elem lejátszik \(t\) darab versenyt, és megszámoljuk, ki hányszor győzött
Kombinatorikai feladatok sajátosságai
A kromoszómák permutációs ábrázolása
A kombinatorikai feladatoknál a permutációs kormoszóma reprezentáció használható. Lásd a Gén reprezentáció részben.
Keresztezés kombinatorikai feladatokban
- Uniform sorrend alapú keresztezés
- két szülőből egy utód, megtartva a gének szülőkön belüli relatív sorrendjét
- lépések (példa a jegyzetben):
- egy véletlen bitmaszkot állít elő, ami ugyanolyan hosszú, mint az egyes kromoszómák
- ahol a bitmaszk értéke 1, oda átmásolja az egyik szülő génjeit
- a második szülő alapján tölti fel a maradék géneket
- sorbaveszi a második szülő azon génjeit, amik még hiányoznak a gyerekből
- ezeket olyan sorrendben tölti fel, ahogy a 2. szülőben vannak
- Edge rekombináció
- a szülőkben a gének szomszédsági viszonyait vizsgálja, ezeket igyekszik átvinni a gyerekbe
- picit hosszú és példa nélkül nehezen érthető, itt van a jegyzetben
Mutáció kombinatorikai feladatokban
- korlátozottabban működnek a mutációs műveletek
- Csere: a kromoszóma két tetszőleges génjét megcseréljük
- Invertálás: kiválasztunk egy szakaszt a kromoszómán belül, és ebben a gének sorrendjét megfordítjuk
16. tétel - Genetikus algoritmus II.
Mutassa be az evolúciós módszerek jellegzetességeit és alapvető lépéseit! Részletesen ismertesse a különféle szelekciós lehetőségeket (elitizmus, csonkolás, rendezett kiválasztás, fitnesz arányos kiválasztás, versengő kiválasztás)! Miként lehet megvalósítani a keresztezést és mutációt?
Evolúciós módszerek jellegzetességei és alapvető lépései
Szelekciós lehetőségek
A szelekció történhet:
- visszahelyezéssel: az egyes elemek többször is részt vehetnek a kiválasztási folyamatban
- visszahelyezés nélkül: egy egyed csak egyszer választható
1. Elitizmus
A populáció legjobb elemei automatikusan átkerülnek a következő populációba.
- a fitnesz értéke így biztosan monoton csökken
- de nagyobb az esélye, hogy beragad egy lokális optimumba.
2. Csonkolás
A legegyszerűbb, determinisztikus módszer.
- Fitnesz szerint sorbarendezzük az elemeket
- Kiválasztjuk a legjobbakat
- A többit eldobjuk
3. Rendezett kiválasztás
Hasonló a csonkoláshoz, de nem determinisztikus. A fitnesz szerint rendezett listában előbb lévő elemek nagyobb valószínűséggel kerülnek kiválasztásra.
Van egy \(k\) paramétere. Ha ez kicsi, jó eséllyel be fognak kerülni a rosszabb elemek is, ha nagy, akkor csak a legjobbak szaporodhatnak.
Egy ciklussal generál \(M_{size}\) darab véletlen számot az alábbi képletekkel:
\[\gamma = \frac{1}{1-\frac{\log{k}}{\log{|M_{size}|}}}\]
\[i = RND_u(0,1)^{\gamma}\cdot|P|\]
Az így kapott \(i\)-t indexként értelmezzük, a populáció \(i.\) eleme bekerül a készülő \(M\) halmazba. Azáltal, hogy \(M_{size}\) darabot generál, telepakolja az \(M\) halmazt.
4. Fitnesz arányos kiválasztás (Rulettkerék módszer)
Az alapelve, hogy a jobb fitnesszel bíró elemek nagyobb eséllyel szaporodjanak.
\(P(p)\) valószínűség adja meg, hogy a kiválasztás során milyen eséllyel választjuk a \(p\) egyedet (minél kisebb a fitnesz, annál jobb az elem, és annál nagyobb esélye van):
\[P(p) = \frac{\frac{1}{f(p)} }{ \sum\limits_{\forall q \in P } \frac{1}{f(q)} }\]
Tehát a populáció összes \(q\) elemére kiszámoljuk \(\frac{1}{f(q)}\) értéket, ezeket összeadjuk, és ehhez viszonyítjuk az adott \(p\) elemmel számolt \(\frac{1}{f(p)}\) értéket. A kapott szám 0 és 1 közötti valószínűség lesz.
Ha kicsi az eltérés a fitneszek között, érdemes lehet a min-max normalizálást használni.
5. Versengő kiválasztás
Felveszünk \(k\) darab egyedet a populációból, és versenyeztetjük őket egymással. A nyertes bekerül a szülő állományba.
\(k\) itt ugyanúgy a szelekciós nyomás, ha kicsi, akkor rosszabb elemek is bekerülhetnek, ha nagy, akkor csak a legjobbak. Ennek oka, hogy az egyedek átlagosan \(k\) darab versenyben fognak részt venni.
Előnye, hogy számszerű fitnesz értékre nincs hozzá szükség.
Továbbfejlesztése, hogy nem a nyertes kerül be biztosan, csak ő kap erre nagyobb esélyt. Például a verseny \(i.\) helyezettje \(p(1-p)^{(i-1)}\) eséllyel választódik ki.
Keresztezés
Amikor kettő vagy több szülő adatai alapján létrehozunk egy egyedet.
1. Bináris keresztezés
- Megadjuk, hogy az egyes kromoszómák hány ponton legyenek szétvágva, majd összeillesztve.
- Alapvetően binárisan kódolt kromoszómákra dolgozták ki.
Fajtái:
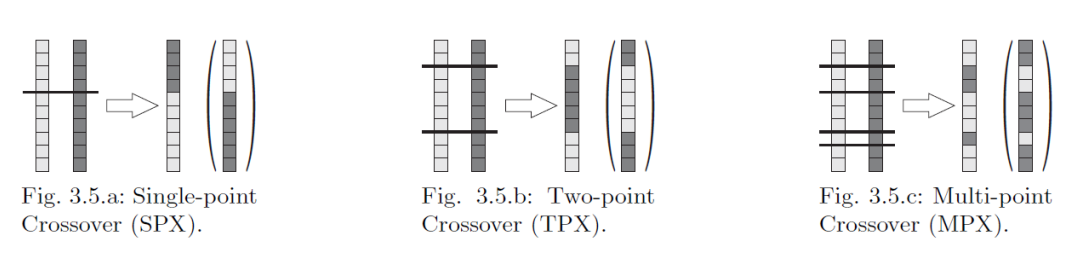
2. Köztes keresztezés
Ha tudjuk, hogy a gének számok, akkor számoknál értelmezett műveleteket hajthatunk rajtuk végre.
Ha \(p_1[i]\)-vel és \(p_2[i]\)-vel jelöljük az első és második szülő \(i.\) génjét, akkor a leszármazott \(i.\) génje kiszámolható:
\[ c[i] = \alpha \cdot p_1[i] + (1-\alpha) \cdot p_2[i] \]
Ahol \(\alpha\) egy véletlen szám az alábbi tartományból:
\[\alpha \in [-h, 1+h] \]
Itt \(h\) egy tetszőlegesen beállítható paraméter, megadja, hogy az új egyed mennyire léphet ki a szülei által megadott tartományból.
Mutáció
- gének értékének egyedi megváltoztatása
- ez ad lehetőséget a lokális optimumokból való kiugrásra
- biztosítja, hogy ne konvergáljon túl gyorsan
- két paramétert szoktunk megadni:
- mutációs ráta: megadja, hogy milyen eséllyel fog megváltozni egy elem
- mutáció mérete: megadja, hogy mekkora méretű mutációk történhetnek
- lehet egy korlát, vagy eloszlás paraméterei, stb.
- a mutáció érinthet:
- egy pontot: a kromoszóma egy génje változik meg
- több pontot: a kromoszóma egymástól független génjei változnak meg
- összefüggő területet: egy jól behatárolt terület génjei változnak meg
- változó hosszúságú kromoszómáknál:
- 1 vagy több elemmel bővülhet a meglévő kromoszóma
- kitörölhetünk egy gént vagy génsorozatot
17. tétel - Genetikus programozás
Milyen esetekben célszerű használni a genetikus programozást? Miként építhető fel a programfa, milyen követelményeknek kell teljesülniük? A módszer miben különbözik a klasszikus genetikus algoritmusoktól (reprezentáció, fitnesz számítás, mutáció)? Milyen genotípus-fenotípus leképezéseket ismer?
Alapelv
- Automatikus programkészítő módszer
- Olyan programot akarunk készíteni, ami a lehető legkisebb hibával tudja megoldani a kitűzött feladatot
- Hasonló a genetikus algoritmushoz
- annyi, hogy itt a keresési tér a lehetséges programok tere
A programfa felépítése
- Az összetett kifejezéseket általában jól lehet reprezentálni egy fával
- A fa levélelemei önmagukban kértékelhető elemek (terminális elemek) lehetnek:
- konstansok,
- változók
- input értékek
- paraméter nélküli függvények
- A fa belső pontjai mindig műveletek
- az alattuk lévő egy vagy több elemmel végeznek el valamilyen műveletet
- az eredményt továbbítják a szülőjük irányába
- a műveletek lehetnek:
- aritmetikai műveletek,
- logikai műveletek,
- vezérlési szerkezetek (if, for, stb.)
- egyéb saját függvények
- A fa gyökérpontja kitüntetett szerepű, ez adja meg a teljes program kimenetét
- a bemeneteket tehát rákapcsoljuk a levélpontokra, majd kiértékeljük a teljes fát
- a terminális elemek a \(T\) halmaz elemei, míg a műveletek az \(F\) halmaz elemei.
Validációs követelmények
\(T\) és \(F\) halmaznak teljesítenie kell az alábbi követelményeket:
- Zártság:
- az egyes műveletek eredménye bemenete lehet bármelyik másik műveletnek
- ez azért fontos, hogy a keresztezés/mutáció során ne álljanak elő szintaktikailag helytelen megoldásjelöltek
- Elegendőség:
- a problémának megoldhatónak kell lennie \(T\) és \(F\) halmaz elemeiből építkezve
Azt is garantálni kell, hogy a programfa kiértékelhető, az általa képviselt program futtatható legyen.
- Célszerű alapból úgy megadni az utasításokat, hogy azok teljesen hibatűrőek legyenek
- tehát egy utasítás ne akadjon el azon, hogy eggyel több vagy kevesebb operandust kapott
- célszerű értelmet adni a valóságban értelmezhetetlen műveleteknek
- pl. 0-val osztás
- a módosított fákat grammatikai elemzésnek vethetjük alá, majd javíthatjuk a hibákat automatikusan
- eleve úgy készíthetjük el a keresztezés és mutáció műveleteket, hogy azok csak szintaktikailag helyes fákat tudjanak létrehozni
- egy másik lehetőség, hogy a kereső algoritmus nem látja közvetlenül a fát, csak egy alacsonyabb szintű reprezentációját
- pl egy bitsorozatot
- a kifejezésfa fenotípus, a genotípus ennek a reprezentációja
- a kettő között megfelelő gpm-mel elérhető, hogy mindig helyes fát kapjunk
Fitnesz
Definiálnunk kell valamilyen formában a fitneszt.
Lehet pl:
- boolean: jól működik / nem működik jól a program
- ennél célszerűbb valami árnyaltabb, hogy a fitnesz arányok felhasználhatóak legyenek
- tanítási minta:
- megadunk egy vagy több elvárt bemenet-kimenet párt
- a feladat olyan program összeállítása, ami a megadott bemenetekre a megadott kimeneteket adja
- a fitnesz ekkor a program által készített kimenetek és a referenciakimenetek távolságainak összege
- szabályok meghatározása:
- megadunk egy szabályt, hogy mit tartunk jó megoldásnak
- pl. útkereső algoritmusnál megadjuk, hogy milyen közelre kell jusson a célponthoz
További részcél lehet, hogy az algoritmus legyen minél rövidebb, futásideje legyen minél kevesebb (ezek csak másodlagos célok általában).
Megvalósítás
Alapvetően teljesen azonos a genetikus algoritmussal, gyakorlatilag ez is egy evolúciós módszer.
Milyen eltérések vannak ahhoz képest?
Kezdőpopuláció létrehozása
Itt is megadott számú véletlen elemet hozunk létre, de általában változó hosszúságú a kromoszóma.
A hosszúságot korlátozhatjuk:
- megadjuk a maximális műveleti darabszámot
- megadjuk a fa maximális mélységét (\(d\))
- ennek megfelelő generálási módszerek:
- full: minden
gyökér → levélút hossza legyen \(d\) - grow: minden
gyökér → levélút hossza legyen maximum \(d\) - ramped half-and-half: a populáció egyik része full, a másik része grow módon lesz generálva
- full: minden
- ennek megfelelő generálási módszerek:
Keresztezés
- Mindkét fát elvágjuk egy ponton
- Az egyik fának megtartjuk a gyökérből kiinduló részét
- A vágási pontra ráillesztjük a másik fa vágás alatti részét
Ez gyakorlatilag a genetikus algoritmusoknál megismert egypontos keresztezés.
Mutáció
Nem fix a kromoszóma méret → sok féle mutációs lehetőség
- Csomópont cseréje egy újra
- \(T\)-beli elemet csak \(T\)-belire, \(F\)-belit csak \(F\)-belire lehet cserélni
- Új csomópontok, részfák beszúrása
- levélből nem lehet belső pontot csinálni, szóval csak a fa belsejébe lehet beszúrni
- Csomópontok, részfadarabok törlése
- belső pontok nem kerülhetnek levél szerepbe
- Művelet gyerekeinek sorrendjének megváltoztatása
Speciális műveletek
Ilyenek nem voltak a genetikus algoritmusnál.
- Fa egyszerűsítése: ugyanazon eredmény elérése kevesebb csomóponttal
- Részfák rögzítése: egy részfa elemeit egységként kezeljük, ekkor terminálisként viselkedik
Genotípus-fenotípus leképezések
JB mapping
- a kromoszóma egész számokból álló tömb
- hagyományosan ezen belül minden utasítás egy számhármas (
opcode,operandus1,operandus2) - előzetesen készítünk egy kódtáblát, hogy melyik azonosító melyik művelethez tartozik, és hogyan használják az operandusokat
- gépi kódhoz hasonlít
Gene Expression Programming
A kromoszóma kupacszerűen tárolja el az adatokat, de a szekvenciálisan tárolt megoldás egy fát reprezentál
- az adatok első fele a fejléc
- ebben lehetnek műveletek és terminálisok is
- a másik fele a farok rész
- ebben már csak terminális lehet
A fa így biztosan valid lesz.
- a műveletek megadják a fa alakját
- a farokrészből csak annyi operandust használ fel, amennyire szüksége van
18. tétel - NSGA variánsok
Ismertesse a többcélú optimalizálás célját és alapfogalmait! Mutassa be az NSGA algoritmus működését! Ismertesse, hogy miben különbözik ettől az NSGAII!
Többcélú optimalizálás célja és alapfogalmai
Lásd a Többcélú optimalizálás tételben.
NSGA I.
A genetikus és raj alapú algoritmusok jól működnek, de egycélú optimalizálásra vannak, erre kínál megoldást az NSGA (Non-Dominated Sorting Genetic Algorithm).
- A Pareto dominancián alapul
- Nem csak egy megoldást, hanem a Pareto frontot adja vissza (optimális megoldások halmaza)
- Arra is törekszik, hogy a visszatérési érték minél jobban lefedje a megoldáshalmazt
Alapelve megegyezik az evolúciós algoritmusoknál tanulttal, csak a szelekcióban különbözik.
A szelekció során a dominancia alapján rakja sorba az elemeket.
- Mindenkinek a jóságát az határozza meg, hogy hányan dominálják
- akiket senki se (első pareto front), azok kerülnek először feldolgozásra
- majd a második pareto front, és így tovább
- az első körben feldolgozott elemek mindig nagyobb fitnesz értéket kapnak, mint a következő frontokban lévők
- akiket senki se (első pareto front), azok kerülnek először feldolgozásra
Egy megosztó függvénnyel próbálja diverzifikálni az eredményeket: előnyben részesíti a frontok azon elemeit, amik kisebb sűrűségű helyen vannak, és hátrányba szorítja a sűrű helyen lévőket.
Megvalósítás

Itt kivételesen a nagyobb fitneszt tekintjük jobbnak.
A megadott algoritmus csak a szelekcióért felelős, tehát bemenetként kapja a \(P\) populációt, a kimenete pedig \(M\) halmazba kerül.
A fő ciklus addig fut, amíg a populáció elemei el nem fogynak. Ebben 3 belső ciklus van:
-
Az első ciklus \(F\) halmazba válogatja \(P\) azon elemeit, akiket nem dominál senki.
- Első esetben ez az első pareto front lesz, utána a második, stb.
- A kiválogatás után ezeket az elemek töröljük a \(P\)-ből.
-
A következő ciklus végzi el a megosztó függvény hívásokat
- Az \(F\) halmaz összes eleménél kiszámolja a többi \(F\) elemhez tartozó távolság összegét
- Ezt helyezi el a \(p_{sh}\) tulajdonságba, majd kiszámolja ezek összegét (\(S_{sh}\))
- Az \(F\) halmaz összes eleménél kiszámolja a többi \(F\) elemhez tartozó távolság összegét
-
A következő ciklus elkezdi kiosztani a fitnesz értékeket az egyes elemeknek
- A fitnesz mindig
fitnessbase-ből indul ki- Ennek a szerepe, hogy az egymást követő frontok egyre rosszabb fitnesz értéket kapjanak
- Ezt módosítjuk a kiszámított sharing értékek alapján
- Minél nagyobb a sharing értéke (tehát minél messzebb van a többiektől), annál nagyobb fitnesz értéket fog kapni
- A fitnesz mindig
A fő ciklusmag végén
- A feldolgozott elemeket hozzáadjuk az \(M\) halmazhoz,
- A a
fitnessbaseértéket lecsökkentjük az aktuális front legkisebb fitneszénél egy kicsivel rosszabb értékre - Hogy mennyivel rosszabbra, azt a
fitnessdeg-gel szabályozzuk, ez legen egynél valamivel kisebb
Megosztó függvény
- Szerepe, hogy a távolságok alapján kiszámoljon egy "sűrűség" értéket.
- Függvény, ami számhoz számot rendel
Egy lehetséges megoldás:
- meghatározunk egy \(\sigma_{share}\) távolságértéket.
- Az ennel messzebb lévő elemekkel nem foglalkozunk (a sűrűség 0)
- a távolságon belüli elemekhez egy lineáris átmenetet adunk meg
- minden elem önmagától vett távolsága 1 legyen
- a \(\sigma_{share}\) távolságra lévő elemhez pedig 0 rendelődjön
Értékelés
Előnyök:
- jó többcélú optimalizálásra
- pareto dominancián alapul
- a pareto frontot adja vissza
- azon belül is a távoli pontokat
Hátrányok:
- érzékeny a szigma értékre
- nincs benne elitizmus
- nagy számításigény
Miben különbözik az NSGA II.?
A feljebb leírt hátrányokra kínál megoldást.
Fast Nondominated Searching Approach
Az NSGA I.-ben az egyes frontok előállításakor minden elemet mindennel össze kell hasonlítani mindennel.
- ennek a lépésszáma \(M \cdot N^3\)
- az NSGA II. ezzel szemben ezt \(M \cdot N^2\) lépésben megoldja
ahol \(N\) a populáció mérete, \(M\) a célfüggvények száma, és legrosszabb esetben minden frontban 1 elem van
Hogyan?
Az első ciklus összehasonít minden elemet (\(p\)) minden másikkal (\(q\)), és kiszámolja az alábbbi értékeket:
npérték: megadja, hogy hány elem dominálja \(p\) megoldást- \(S_p\) halmaz: megadja azokat az elemeket, amiket a \(p\) dominál
Eközben a Pareto frontot (akiket senki sem dominál) kigyűjti \(F\) halmazba.
Ezt követően el lehetkezdeni megadni az egymást követő Pareto-frontok elemeit. Ehhez végigmegy \(F\)-en, ami az éppen aktuális front elemeit tartalmazza.
- Ezeknél eltároljuk a
prank-ba, hogy hányadik frontban vannak - Végignézzük az elemeknek az \(S_p\) halmazát, és az összes ott lévő \(q\) elem
npértékét csökkentjük 1-gyel - Ha valakinek az
npértéke 0-ra vált, az azt jelenti, hogy ő a következő Pareto frontban lesz → betesszük \(F'\)-be - Ezeket ismételjük az újabb és újabb frontra
Sűrűség becslés
Az NSGA II. megpróbálja megbecsülni az egyes elemek környezetének sűrűségét.
- Az első célfüggvény alapján sorbarakja az aktuális Pareto front elemeit
- Minden elemhez kiszámol egy
idistancetávolságot ami- a két szélső elemnél \(∞\),
- a többieknél a kétoldali közvetlen szomszédok távolságából számolható ki
- ezeket az értékeket összegzi az összes célfüggvény esetén, és ezek összege ad egy sűrűségi becslést(
pdist)
- Minél kisebb
pdist, annál nagyobb a sűrűség.
Szelekció
- Minden elemnek megvan a Pareto rangja és a crowding distance értéke
- Egy \(p\) elem akkor dominálja \(q\) elemet, ha
- \(p\) rangja (
prank) kisebb, mint \(q\) rangja (korábbi frontban volt)- vagy ha ez egyenlő, akkor \(p\) sűrűsége kisebb
- \(p\) rangja (
- A szelekciónál ha nem fér minden elem a frontból a populációba, akkor a sűrűség dönt közöttük
TODO: ez a tétel még nincs teljesen kész, az NSGAII-ről még lehet kéne több minden
19. tétel - Raj alapú módszerek
Mutassa be a raj alapú módszerek jellemzőit! Részleteiben ismertesse a Particle Swarm Optimization eljárást! Milyen jellemzőik vannak az egyes egyedeknek és a populációnak? Mi történik az egyes iterációkban? Értékelje a módszert!
Alapelv
- Biológiailag inspirált algoritmusok, a madár- és hajrajok mozgásán alapulnak.
- Ezek az állatok képesek a hatékony együtt mozgásra, pedig nincs kitüntetett vezető, aki irányítana
- Minden pozícióhoz hozzárendelünk egy fitnesz értéket
- A raj célja, hogy minél közelebb kerüljenek az alacsonyabb fitneszű területekhez az alábbi szabályok betartásával:
- az egyedek között nincs kitüntetett vezető
- mindenki ismeri a raj által eddig elért legjobb pontot (globális optimum)
- mindenki ismeri az önmaga által eddig elért legjobb pontot (lokális optimum)
- Tehát itt a globális és lokális optimum mást jelent, mint ahogy eddig használtuk.
- Egy véletlen kiindulópont és kiértékelés után az egyedek mozogni kezdenek.
- Ehhez súlyozottan figyelembe veszik:
- az eddigi mozgási irányukat,
- a globális optimum helyét, és
- a lokális optimum helyét,
- ezek alapján állapítják meg a pillanatnyi sebességüket.
- Ehhez súlyozottan figyelembe veszik:
Megvalósítás
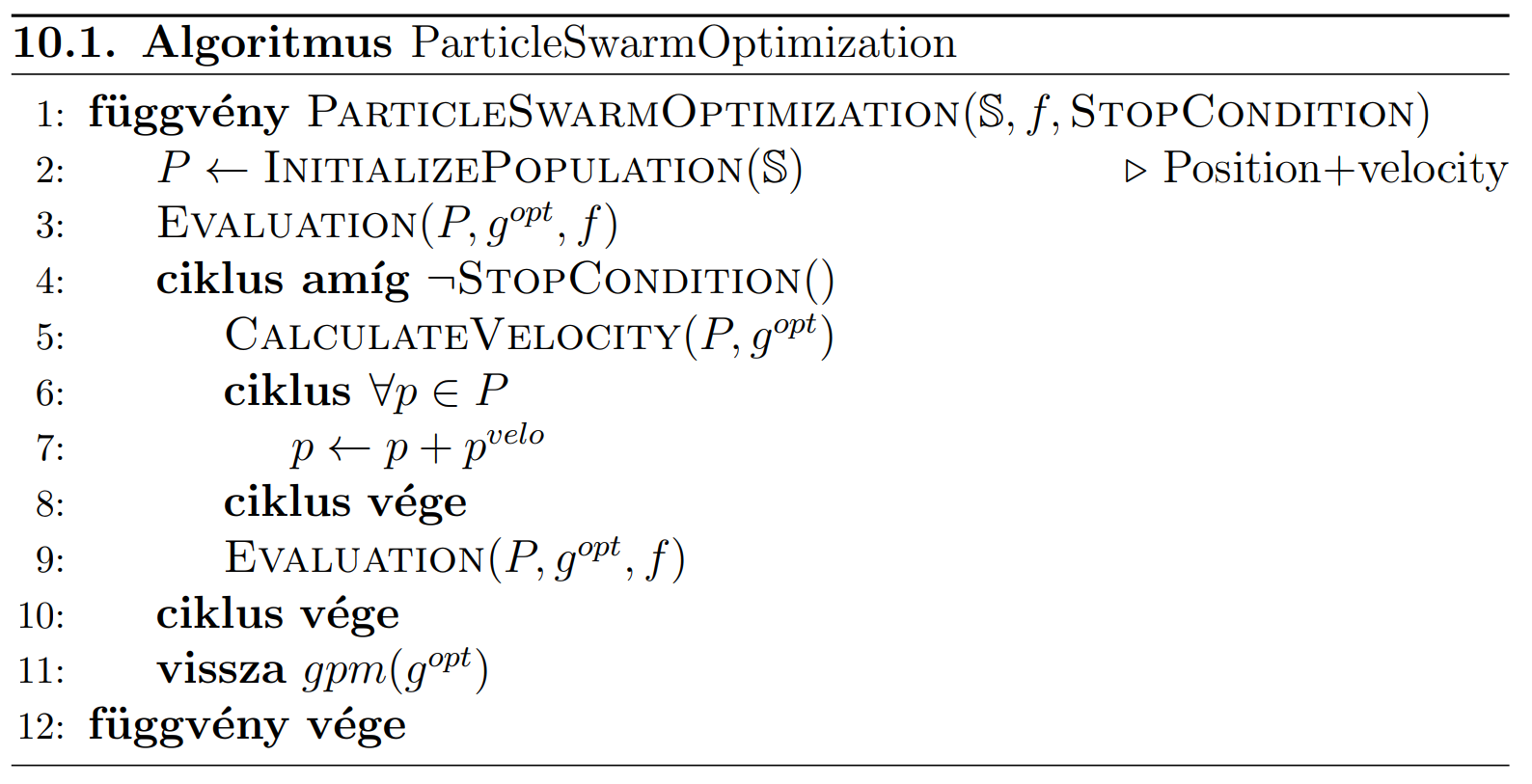

A rendszer lépései
Folyamatábra
flowchart TB
IN["`**Inicializálás**
*(kezdőpontok, kezdősebességek)*`"] --> EV
EV["`**Kiértékelés**
*(optimumok esetleges módosítása itt történik)*`"]
STOPCOND{"Megállási feltétel teljesül?"}--"igen"-->STOP
V["Sebességek meghatározása"] --> M
M["Mozgatás"] --> EV --> STOPCOND --"nem"--> V
STOP["Leállás, vissza gpm(g_opt)"]
-
Inicializálás: A keresési térben véletlenszerűen kiválasztjuk a kezdőpozíciókat és kezdősebességeket.
-
Kiértékelés:: Minden egyed megállaptíja a saját fitneszét, majd ennek megfelelően módosítja a globális és lokális optimumok értékét
-
Sebességek meghatározása: Minden egyed megállapítja a saját sebességvektorát. Ehhez figyelembe tudja venni az aktuális pozícióját, sebességét, illetve a globális és lokális optimumokat.
-
Mozgatás: A sebességnek megfelelően módosítjuka pozíciót
-
Kiértékelés: Újra kiértékeljük az egyedeket, szükség esetén módosítva a globális és lokális optimumok értékét.
-
A fenti lépéseket addig ismételjük, amíg nem teljesül valamelyik megállási feltétel.
A függvény visszatérési értéke a globális optimumhoz tartozó problématérbeli megoldás lesz.
A sebesség meghatározása
A sebesség fogalom bármi lehet, de támogatnia kell az alábbi követelményeket:
- két pozíció különbsége egy sebesség legyen
- sebességet meg lehessen szorozni egy skalár értékkel
- össze lehessen adni két sebességet
- egy pozícióhoz hozzá lehessen adni egy sebességet
Az új sebesség megállapítás jellemzően az alábbiakon alapul:
- jelenlegi sebesség
- globális optimum iránya az aktuális pozíciótól
- lokális optimum iránya az aktuális pozíciótól
Ezeket a tényezőket súlyozzuk, esetleg véletlen számokkal kombináljuk.

Értékelés
Előnyök
- Nagy keresési tereknél jó, jól át tudja fésülni
- Amikor közelít a globális optimumhoz, lassulnak az egyedek (az átlagszámításnak megfelelően)
- Jól párhuzamosítható
Hátrányok
- Sok paramétere van, nehezen konfigurálható
- Csak szám keresési terekben működik
20. tétel - Klaszterezés
Mit értünk klaszterezési feladatok alatt? Mutassa be a K-means algoritmust! Ismertesse a DBSCAN algoritmus alapfogalmait és alapvető lépéseit! Mi a különbség az egyes módszerek között?
Klaszterezési feladatok
- A klaszterezés közeli adatokból csoportokat (klasztereket) alakít ki.
- Az egymástól távoli elemek különböző klaszterekbe kerülnek.
- Gyakran a csoportok elhelyezkedése és száma előre nem ismert
flowchart TB K[Klaszterezés]-->H[Hierarchikus] & NH[Nem hierarchikus] H --> O["`**Összevonó** *(kezdetben minden elem külön klaszter, majd ezeket összevonogatja nagyobb klaszterekké)*`"] H --> F["`**Felosztó** *(kezdetben az összes elem egy klaszterben van, és ezt bontogatja kisebb klaszterekre)*`"] O --> DS[DBSCAN] NH --> KM["K-means"]
K-közép (K-means) algoritmus
- Nem hierarchikus
- \(N\) darab centroidot tárol (\(C_1\), \(C_2\), ... \(C_n\))
- Minden pont abba klaszterbe (\(K_1\), \(K_2\), ... \(K_n\)) tartozik, amelynek a centroidjához legközelebb van
- Úgy mozgatja a centroidokat, hogy minél inkább egymástól elkülönülő klaszterek jöjjenek létre
Alapvető lépések
- Inicializálás, kezdő centroidok (klaszterek ”középpontjának”) megadása
- tipikusan véletlenszerűen
- Elemek besorolása a klaszterekbe a távolsági adatok alapján
- minden elem a hozzá legközelebbi centroid klaszterébe kerül.
- Ez alapján klaszterek középpontjának módosítása -minden centroid új pozíciója a hozzá tartozó elemek pozícióinak átlaga lesz
- Ha változtak a középpontok, akkor megismételjük a műveletet.
- Ha nem változtak a középpontok, kilép az eljárás
Folyamatábra
flowchart TB
I["Inicializálás (véletlen kezdőpontok felvétele)"]
BES[Elemek besorolása a klaszterekbe a távolságok alapján]
KP["Centroidok módosítása (a klaszterbe tartozó elemek pozíciójának átlagolásával)"]
V{Változtak a centroidok?}--"igen"-->BES
I-->BES-->KP-->V--"nem"-->K[Kilépés]
Megvalósítás

- \(C'\) halmaz mindig az előző iteráció elemeit tárolja
- ide hozzuk létre a kezdő centroidokat is
- Az új centroidokat mindig a \(C\) halmazba hozzuk létre
- \(K\) halmazok tárolják a klaszterek elemeit
- ezeket mindig újra létrehozzuk
- A függvény visszatérési értéke a klaszterek halmaza
Értékelés
- Előny: Egyszerű, gyors
- Hátrány: előre meg kell adni a klaszterek számát, amit sokszor nem tudunk
- Kiegészítési lehetőség: ha ezt nem tudjuk, az algoritmust le lehet futtatni egymás után többféle K értékkel
- Gyakorlati probléma: képszegmentálás
DBSCAN
- Sűrűség-alapú klaszterezési eljárás
- Hierarchikus, öszevonó jellegű módszer
Bemenetei
| Jel | Magyarázat |
|---|---|
| \(S\) | pontok halmaza, amiben keresünk |
| \(d_s\) | két pont távolságát megadó függvény |
| \(minPts\) | minimális darabszám |
| \(\epsilon\) | maximális távolság |
Fogalmak
- Belső pont: olyan pont, amitől a legfeljebb \(\epsilon\) távolságra lévő elemek száma legalább \(minPts\)
- Közvetlenül sűrű elérhetőség: ha egy belső ponttól egy \(q\) pont távolsága legfeljebb \(\epsilon\), akkor \(q\) közvetlenül sűrűn elérhető
- Sűrű elérhetőség: ha egy belső pontból át tudunk "lépkedni" \(q\)-ig úgy, hogy a köztes pontok mindig közvetlenül sűrűn elérhetőek az előző pontból, akkor \(q\) sűrűn elérhető
- tehát a közvetlen sűrű elérhetőség tranzitív lezártja
- Kivülállók: azok a pontok, amelyek nem elérhetőek a többi pontból
Alapvető lépések
- Vegyük azokat a pontokat, amelyeknek az \(\epsilon\) környezetében legalább \(minPts\) darab másik pont található.
- Ezeket a belső pontokat és az \(\epsilon\) környezetben lévő pontokat tekinthetjük egy klaszter kiinduló halmazának.
- Amennyiben vannak a térben olyan pontok, amelyek még nem részei ennek a halmaznak, viszont annak valamelyik belső pontjától \(\epsilon\) távolságon belül vannak, akkor ezekkel egészítsük ki a halmazt.
- Amennyiben már nem találunk ilyen pontot, megkaptuk a kezdőpontból elérhető legnagyobb klasztert.
- Végezzük el a műveletet a többi belső pontra.
A klaszterek átfedhetik egymást.
- Tipikusan az egy klaszter különböző pontjaiból induló keresések átfedő eredményeket adnak.
- Ezért menet közben csak olyan kezdőpontokat választunk, illetve olyan elemekkel bővítünk, amelyek még nem lettek feldolgozva.
K-means és DBSCAN különbségei
| K-means | DBSCAN | |
|---|---|---|
| Típus | Nem hierarchikus | Hierarchikus, összevonó |
| A klaszterek számát... | tudni kell előre | nem kell tudni előre |
| Zajkezelés | A zajt is klaszterbe akarja rakni | Jól kezeli a zajt, a kívülállók nem kerülnek klaszterbe |
| Számításigény | Nem különösebben számításigényes | Sok elem esetén meglehetősen számításigényes |

21. tétel - Grafikus kártyák felépítése
Minek köszönhető az általánosan programozható grafikus kártyák léte? Miben különbözik a GPU és a CPU hardver programozói szemmel (cache, memory latency hiding, stb.)? Milyen specialitásokkal és korlátokkal bír a GPU hardver (SIMT végrehajtás, memória, stb.)? Milyen jellegű feladatoknál célszerű használni a GPU-t?
GPU-k fejlődése
A GPU-k megjelenését jelentősen befolyásolta a 3D grafika megjelenése.
- A 3D térből az objektumok leképezése a 2D síkra az objektumok háromszögekre való bontásával történik
- Ezek a pontok egymástól függetlenek → jól párhuzamosítható a GPU sok végrehajtó egységén
- Különféle 3D grafikák más-más workloaddal járnak → shaderek számát nehéz optimalizálni
- Probléma áthidalható Unified Shader-rel: egyfajta shader, teljesen általánosan használható végrehajtó egységekkel
- Ezzel a hardver rendelkezésre állt, megjelent a GPGPU (General Purpose Computing on GPUs)
- Kezdetben kódot írni nehézkes volt → azóta a GPU gyártók driverekkel, framework-ökkel segítenek.
CPU-GPU különbségek
| CPU | GPU |
|---|---|
| Nagy teljesítményű ALU-k | Energiahatékony ALU-k, de nagyon sok |
| Relatíve nagy cache, hogy ne kelljen mindig a memórához nyúlni | Relative kis cache |
| Bonyolult és hatékony vezérlés: branch prediction, data forwarding, stb. | Egyszerű vezérlés: nincs branch prediction vagy data forwarding |
| Gyors kontextusváltás: az adatok a szálakhoz vannak rendelve, nem kell őket másolgatni kontextusváltáskor |
Memory Latency Hiding
- A végrehajtó egységeknek sok adatra van szüksége
- A memóriasebességek lassabban nőnek, mint a számítási teljesítmény.
- Elkerülendő, hogy a feldolgozás adathiány miatt várakozzon.
| Hogyan oldja meg ezt a CPU? | Hogyan oldja meg a GPU? |
|---|---|
Bonyolult és hatékony utasítás- és elágazás-előrejelzéssel.
| Nincsenek ilyen kifinomult módszerek. Ha az egyik szál megakad, mert adat kell a memóriából:
Ehhez persze több szál kell, 1 szál esetén nem működik. |
Specialitások és korlátok
SIMT végrehajtás
A GPU-kban csak egy utasításértelmező/vezérlő tartozik a VE-khez → egyidőben minden VE csak ugyanazt az utasítást hajthatja végre (más adaton).
- A SIMT a SIMD-hez hasonló, egymás melletti szálak itt is azonos utasítást hajtanak végre
- azonban a SIMD-től eltérően nem csak egymás melletti adatokon tud dolgozni.
- De mi van akkor, ha egy kódban van elágazás?
- valamelyik szálnak az igaz, valamelyiknek a hamis ágat kell lefuttatni, de csak ugyanazt képesek egyszerre végrehajtani
- megoldás:
- míg bizonyos ágak az igaz ágat futtatják, a többi kikapcsol, majd fordítva
- eredmény: sokkal rosszabb teljesítmény
Memória
A GPU-nak külön memórája van.
- ide át kell másolni azokat az adatokat, amikkel a számítást kell végezni
- a másolás időigénye miatt sokszor értelmét veszti a GPU végrehajtás
Megoldás: úgy kell megírni a kódot, hogy minél jobban elkerüljük a költséges adatmásolásokat. Például a véletlen számokat a GPU-n hozzuk létre, nem a CPU-ról másoljuk.
Milyen jellegű feladatoknál célszerű használni a GPU-t?
- nagy számításigényű feladatoknál, ahol nagyon sok szálat kell indítani.
- olyan feladatoknál, amik jól párhuzamosíthatóak (pl. szálak között nincs függőség).
Előnyök
- magas csúcsteljesítmény
- jó ár-érték arány
- skálázható
- dinamikusan fejlődő (játékipar)
Hátrányok
- adatmásolások miatti korlátok
- GPGPU programozás eléggé új terület, így költségesebb vele foglalkozni
22. tétel - Végrehajtás a grafikus kártyán
Miben különbözik a CPU és GPU futtatási rendszere, hogyan lehet a GPU-n szálakat indítani és paraméterezni? Ismertesse a blokk fogalmát (használata, szinkronizáció, shared memory)!
- Alapvetően a CPU-k soros feldolgozásra összpontosítanak, összetett utasításkészlettel rendelkeznek
- A GPU-k párhuzamos feldolgozásra vannak optimalizálva, utasításkészletük specifikusabb, szűkebb
Maga a CUDA Runtime 3 komponenscsoportot biztosít az alap C nyelvi elemeken felül:
| Általános komponensek | Hoszt komponensek | Eszköz komponensek |
|---|---|---|
| A GPU és CPU kódban is használhatóak. | Csak a CPU kódban használhatóak (memóriafoglalás, GPU-ra másolás, kernel irányítás, stb.). | Csak a GPU kernel kódjában használhatóak. |
- A GPU-n futó kód a számítógép legtöbb komponenséhez nem fér hozzá (pl. háttértár, fájlkezelés.)
- A kivételkezelés is más, hiszen a hoszt oldali kivételektől eltérően semmiféle visszajelzés nem jön ezekről.
- Fontos a függvények visszatérési értékét ellenőrizni, hogy nem történt-e hiba a GPU-s végrehajtás során
Kernel
- A szálak indításához kernelre van szükség
- A kernel lényegében egy C függvény, meghívásakor a GPU szálain végrehajtásra kerül
- Szintaktikailag azonos, de el kell látni speciális kulcsszavakkal
- pl:
__global__: a belépési pontot jelöli, meghívható a hosztról
- pl:
- A kernelen belül bizonyos hoszt funkciók nem érhetőek el, mint pl. fájlkezelés
- A kernel indításához speciális szintaktikával kell meghívni a kernel függvényt
- blokkok és szálak számát meg kell adni
- lehet átadni paramétereket, de minden szál ugyanazokat kapja meg
- A kernelen belül lekérhető az adot szál indexe
- vagy indexei, ha több dimenziós blokkban van**
- Van szinkronizáló eljárás
- amikor egy szál eljut egy ilyen híváshoz, várni fog addig, míg azt a többi szál is eléri pontosan ugyanazt az eljárást
- ezzel könnyű holtpontot okozni (pl. elágazásnál)
- amikor egy szál eljut egy ilyen híváshoz, várni fog addig, míg azt a többi szál is eléri pontosan ugyanazt az eljárást
Blokkok
- a szálak blokkokba vannak rendezve
- a GPU a blokkokat függetlenül kezeli
- nem lehet köztük szinkronizálni, hatékonyan adatot megosztani
- néhány nagyon modern GPU-nál lehetséges a blokkok közötti szinkronizáció, de csak erős fizikai korlátok között (pl. egyszerre kell futniuk)
- az egy blokkon belül futtatott szálak száma korlátozott (ma tipikusan 1024)
- ha ennél több szál kell, akkor több blokk is kell
- egy GPU több streaming multiprocesszort tartalmaz
- egy blokk csak egy ilyenen futhat
- könnyen lehet, hogy a blokkok nem egyszerre futnak le hardveres korlátok miatt
A blokkok összessége a grid: ezen belül a blokkoknak szintén van indexe.
- többdimenzióban is lehet a blokkokat is indítani, mint a szálakat
- így egy szálnak van globális + lokális azonosítója is
A szükséges blokkok száma (\(BM\) = blokkméret, pl. 1024):
\[\Bigl\lfloor\frac{szálak-1}{BM}\Bigr\rfloor+1\]
Blokkok közötti szinkronizáció alternatív megoldása
- Kritikus pontnál kettébontjuk a kernelt
- A kettő új kernelt külön kell meghívni
- A szinkronizáció a CPU-nál történik
- lehet addig blokkolni a CPU-t, ameddig minden munka befejeződik a GPU-n
- a CPU blokkolása nem hasznos, de ez a megoldás, ha nagy szükség van a szinkronizációra
Shared memória
- A GPU 3 féle memóriájának (device/global, shared, szálak saját változói) egyike
- Hardver oldalról: a streaming multiprocesszor belső memóriája
- Programozói oldalról: minden blokknak saját shared memóriája van
- Adatok beolvasása innen sokkal gyorsabb, mint a globális memóriából
- A mérete azonban sokkal kisebb is, kb 48kB
- Az egy blokkon belüli szálak látják, ezen keresztül tudnak hatékonyan kommunikálni
- speciális kulcsszó kell hozzá (
__shared__) - Előnyös használni:
- Memóriahozzáférések csökkentésére (ha minden szálnak ugyanaz az adat kell, érdemes ide másolni)
- Szálak egymás közti kommunikációjára
- Nem előnyös: ha minden szál más adathoz akar hozzáférni, azokhoz is kevésszer
23. tétel - Grafikus kártya memória felépítése
Milyen memóriaterületek jelennek meg egy grafikus kártyán? Mikor és milyen módon célszerű ezeket használni? Mutasson konkrét példát a shared memória használatára (pl. tiled matrix)!
Memóriaterületek
A GPU-n belül több streaming multiprocesszor van. Ezeken belül több VE található.
Két nagy memória csoport:
- On-chip memóriatartomány (multiprocesszoron belüli memóriatartomány)
- Off-chip memóriatartomány (GPU saját memóriája, pl. 12GB)
| On-chip memóriatartomány | Off-chip memóriatartomány |
|---|---|
|
|
* valójában off-chip, de ide soroljuk
| Fizikai felépítés | A programozó szemszögéből |
|---|---|
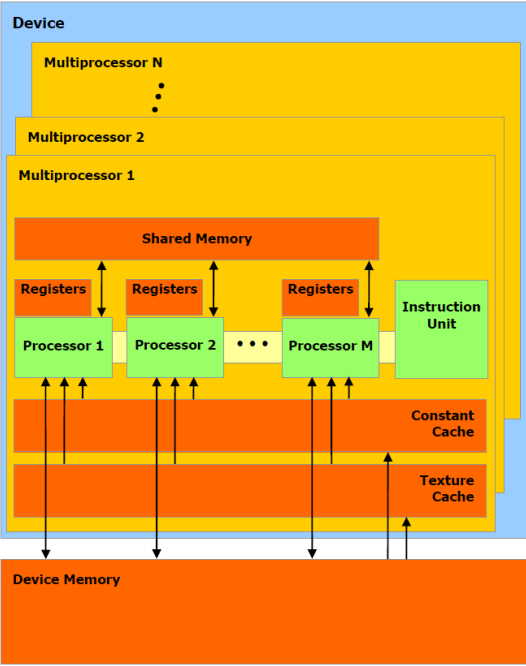 | 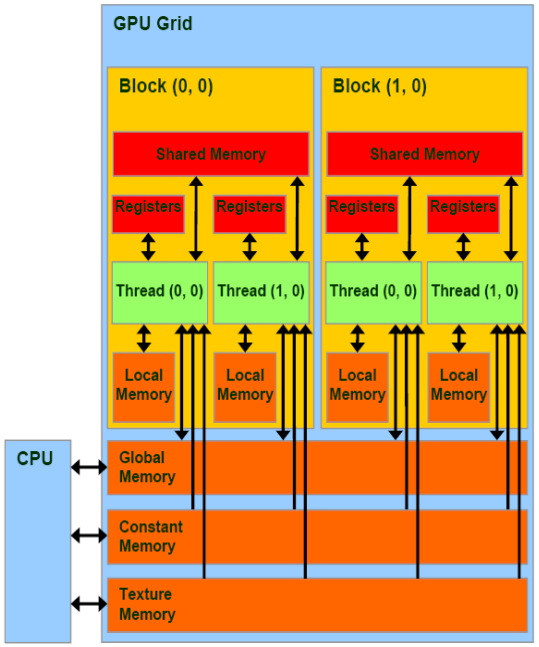 |
Off-chip tartomány
Részei:
- globális memória
- konstans memória
- textúra memória
- rögzített memória
- zero-copy memória
Globális memória
- élettartam: program futása
- a blokkok, a szálak és a hoszt is hozzáfér
- nagy, de relatíve lassú
Konstans memória
- hasonló a globálishoz
- a szálak számára csak olvasható
- az adatok cachelve vannak, így gyorsabb tud lenni a globálisnál
- célszerű használni, ha az adat nem lesz módosítva (pl. szövegben való keresés)
Textúra memóra
- fizikailag a globális memóriával egyező tartomány
- lényeges különbség, hogy máshogyan van kezelve
- grafikához, textúrához alakított műveletek, stb.
Rögzített memória
- a hoszt oldalon foglalható
- garantálja, hogy az adat az operatív tárban marad, nem kerül a háttértárba
- ezáltal gyorsabb a másolás
- enélkül is lehet másolni, de a GPU mindenképpen létrehoz egy ilyet biztonsági okokból
- előbb ide másolódik át az adat, csak utána a GPU-ra
Zero-copy memória
- vannak olyan átfedett memória területek, amiket a CPU és GPU is lát és tud kezelni
- a zero-copy erre a területre foglal memóriát
- tipikusan gyengébb eszközöknél fordul elő, ahol a GPU-nak nincs saját memóriája
On-Chip memóriatartomány
Regiszterek
- élettartam: szűk élettartam
- csak az őt birtokló szál fér hozzá
- tényleges műveletvégzés itt történik
- nagyon gyors, de kevés van belőle
- 1 változó = 1 regiszter
Lokális memória
- valójában off chip, de a regiszterekhez nagyon hasonló (egy szálhoz tartoznak)
- ha elfogynak egy szál regiszterei, akkor ezek használhatóak
- fizikailag a globális memória része, innen kerül lefoglalásra
Shared memória
- sebessége kb. a regiszterekkel egyező, mérete relatíve kicsi (~48kB)
- blokkokhoz kapcsolódik, szálak közötti kommunikációra tökéletes
- hoszt oldalról nem elérhető
- célszerű cache-ként használni a sok szál által sűrűn használt adatokhoz
Shared memória használata: csempézett mátrix-szorzás
Ez részletesen le van írva ábrákkal itt.
24. tétel - Optimalizálás a grafikus kártyán
Mik az optimális GPU kód jellemzői (szálak, elágazások, adat/számítás arány, occupancy)? Hogyan választható meg az optimális blokkméret? Atomi műveleteket hogyan lehet helyettesíteni?
Szálak
- A szálak blokkokba szerveződnek
- Az egy blokkon belül futtatható szálak száma korlátos (pl. 1024)
- tehát ennél több szálhoz több blokk kell
- A fizikai futtatás warponként történik
- warp: a blokkok felbontásra kerülnek 32 szálas részekre
- a multiprocesszorok folyamatosan figyelik, hogy melyik warp futtatható
- ha elakad egy warp, próbál másikra váltani → ha nem tud, akkor kihasználatlanul áll
- ezért fontos, hogy a szálak minél jobban párhuzamosítva legyenek (függetlenek legyenek)
- ha elakad egy warp, próbál másikra váltani → ha nem tud, akkor kihasználatlanul áll
Elágazások
- A GPU-n belül egy vezérlő tartozik a VE-khez → egyidőben csak ugyanazt az utasítást tudják végrehajtani
- SIMT végrehajtás → pl. míg bizonyos szálak az igaz ágat futtatják, a többi kikapcsol, majd fordítva
- mivel ez rosszabb teljesítményt okoz, törekedni kell a minél kevesebb elágazás használatára a kódban
Adat-számítás arány
- minden multiprocesszoron belül korlátozott mennyiségű memória van
- ha a warpok túl sok regisztert és memórát használnak, kevesebb warpot tud futtatni egyszerre a multiprocesszor
- fontos tehát csak a szükséges méretű memóriát használni, optimalizálni
Occupancy
- a warpok mérete 32 → célszerű 32-vel osztható blokkméretet választani
- pl. ha marad 16 szál, az ugyanúgy 1 warpot fog elfoglalni → rosszabb kihazsnáltság
- finoman szemcsézettség megfontolása:
- pl. annyi a feladat, hogy 1030 szál végezzen egymástól független számításokat
- ekkor jobb kihasználtság érhető el, ha 2db 515 szálas blokkot használunk, mintha 1db 1024 + 1db 6 szálasat használnánk
Atomi műveletek helyettesítése
- probléma: két szál akar egyszerre atomi műveletet végerehajtani ugyanazon a memóriacímen → szerializálni kell, ami lassítja a végrehajtást
- a cél a lehető legkevesebb atomi művelet használata (nem mindig kerülhető el)
- a helyettesítés történhet pl. redukcióval
- minimumkiválasztás: \(\frac{N}{2}\) szál összehsonlít → szinkronizál → \(\frac{N}{4}\) szál összehasonlít, stb.
- a végén megkapjuk a min. elemet
- shared memóriával gyorsíthatjuk tovább
- minimumkiválasztás: \(\frac{N}{2}\) szál összehsonlít → szinkronizál → \(\frac{N}{4}\) szál összehasonlít, stb.